Арифметическое линейное пространство

Рассмотрим множество 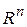всех (строк из 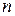элементов) действительных чисел . Введем на этом множестве умножение числа на и сложение так:

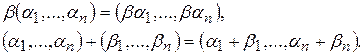
Ниже будем называть векторами, и обозначать латинскими буквами возможно с нижними индексами. Исключение составит нулевой вектор . Числа из 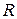будем обозначать греческими буквами

Множество 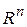, вместе со сложением векторов и умножение числа на вектор образуют арифметическое линейное пространство или 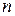- мерным векторным пространством.

Непосредственно из определения следуют такие свойства сложения векторов в :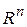

Умножение числа на вектор обладает следующими свойствами:

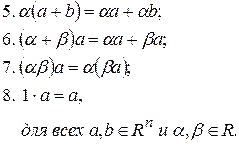
Из этих свойств следует, что в сумме нескольких векторов не обязательно расставлять скобки (свойство 1) и она не зависит от порядка следования слагаемых (свойство 4). В сумме векторов можно приводить подобные члены, т.е. , а также в равенстве двух сумм переносить вектор из одной части в другую с противоположным знаком.

Справедливы также следующие два утверждения:

(1) .

Действительно,

.

(2) .

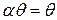Действительно,

.

Вектор вида называется линейной комбинацией векторов (с коэффициентами ). Говорят, что система векторов является линейно независимой, если для любых чисел равенство влечет, что . В противном случае система векторов называться линейно зависимой. Равносильно, система векторов линейно зависима, если найдутся числа , не все из которых равны , но . Равенство можно выразить словами: линейная комбинация векторов с коэффициентами равна нулевому вектору.

ЛЕММА 1 (о линейно зависимых системах). Система векторов линейно зависима тогда и только тогда, когда один из них линейно выражается через предыдущие (тем более, через оставшиеся).

ДОКАЗАТЕЛЬСТВО. Пусть , но не все числа равны , а - наибольший из индексов таких, что .

Тогда 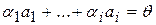, откуда

Обратно, пусть .

Тогда и видно, что в этой линейной комбинации векторов , которая равна нулевому вектору, коэффициент при не равен нулю. □

Система векторов называется системой порождающих (или образующих) линейного пространства , если любой вектор из равен подходящей их линейной комбинации.

ЛЕММА 2 (о порождающих). Если система порождающих линейно зависима, то из неё можно удалить подходящий вектор такой, что оставшаяся система векторов также будет системой порождающих.

ДОКАЗАТЕЛЬСТВО. Если система порождающих линейно зависима, то по лемме 1 в ней найдётся некоторый вектор 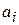, который выражается через :

(1)

Так как для всякого 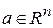найдутся числа такие, что

. (2)

Подставляя в равенство (2) вместо 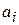его выражение из (1), раскрывая скобки и приводя подобные слагаемые, убедимся в справедливости утверждения леммы. □

Линейно независимая система порождающих называется базисом .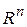

Нетрудно понять, что следующая система векторов будет базисом в :

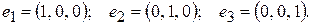
Действительно, она линейно независима, т. к. никакой вектор в ней не может быть выражен через предыдущие. С другой стороны, вектор имеет вид 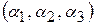и тогда

.

Аналогично, для любого в 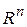существует базис из 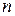векторов, называемых единичными:

ТЕОРЕМА (о базисах). Любые два базиса линейного пространства состоят из одного итого же числа векторов.

ДОКАЗАТЕЛЬСТВО.Пусть даны два базиса линейного пространства и , причем . Рассмотрим систему

.

Она линейно зависима по лемме 1, т.к. выражается через , но разумеется также является системой порождающих. По лемме 2 из нее можно вычеркнуть некоторый вектор, выражающийся через предыдущие, получив систему порождающих

(3)

Рассмотрим систему порождающих

(4)

которая линейно зависима, т.к. выражается через систему (3). По лемме 2 из нее можно вычеркнуть некоторый вектор, линейно выражающийся через предыдущие, получив систему порождающих

При этом вектор (и ) не будет вычеркнут, т.к. в системе никакой вектор не выражается через предыдущие. Затем, рассматриваем систему порождающих

и продолжаем аналогичную процедуру. Т.к. , то в конце концов получим систему порождающих

(5)

причем . Следовательно, вектор линейно выражается через систему векторов (5), что противоречит линейной независимости □

СЛЕДСТВИЕ 1. В пространстве 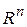любые два базиса состоят из n векторов. □

СЛЕДСТВИЕ2. Любая линейно независимая система векторов дополняема до базиса.

ДОКАЗАТЕЛЬСТВО. Припишем к линейно независимой системе векторов справа векторы , составляющие базис, получив систему . Теперь начнем из этой системы вычёркивать, пока это возможно, векторы, линейно выражающиеся через предыдущие. По лемме 1 векторы вида 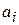вычеркнуты быть не могут, а по лемме 2 оставшаяся система будет и системой порождающих. □

СЛЕДСТВИЕ3. Каждая система порождающих содержит базис. Доказательство аналогично предыдущему. □

СЛЕДСТВИЕ4. В 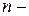мерном линейном пространстве любые векторов образуют линейно зависимую систему.

Доказательство следует из следствия 1 и теоремы о базисах. □

Линейно независимая система векторов называется максимальной, если при добавлении к ней еще одного вектора она становится линейно зависимой. Поэтому базис можно определить как максимальную линейно независимую систему векторов.