Пример 7. Дана матрица . Её определитель , поэтому обратная матрица существует

Дана матрица 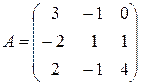. Её определитель 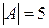, поэтому обратная матрица 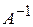существует. Найдём алгебраические дополнения элементов матрицы :

;

;

;

;

.

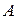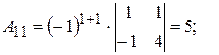
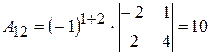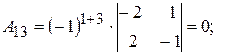
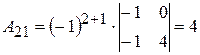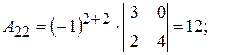
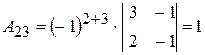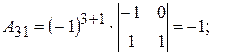
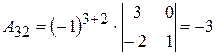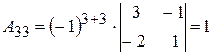Тогда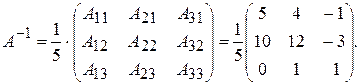

Линейным уравнением от 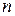неизвестных 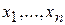называется уравнением вида

.

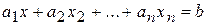Поэтому системой линейных уравнений (СЛУ) называется система вида

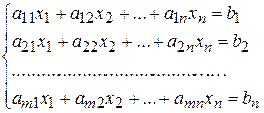(5)

Эта СЛУ состоит из 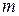уравнений от 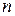неизвестных. Матрица 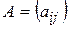, составленная из коэффициентов при неизвестных, называется основной, а если к ней приписать столбец из - свободных членов СЛУ (5), то полученную матрицу называют расширенной. СЛУ (5) можно записать и в матричном виде

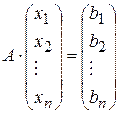(6)

СЛУ (5) называется крамеровской, если число уравнений в ней равно числу неизвестных 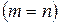и основная матрица ее невырожденная.

ПРАВИЛО КРАМЕРА. Крамеровская СЛУ имеет единственное решение 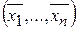, которое находится по формулам

,

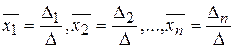где 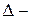определитель основной матрицы СЛУ, а 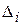получается из 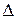в результате замены в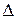 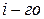столбца на столбец из свободных членов.

ДОКАЗАТЕЛЬСТВО. Так как 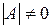, то существует обратная матрица 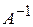. Домножая обе части равенства (6) слева на 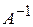, получим

(7)

Вспоминая, чему равна матрица 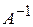и находя произведение в правой части (7) получаем

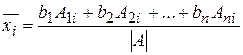(8)

Но по следствию 1 из теоремы Лапласа числитель (7) есть 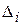, если вычислить 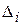, разлагая 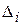по 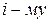столбцу. □

Пример 8. Решить систему уравнений

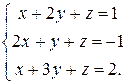
Решение.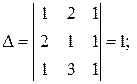

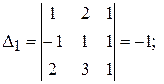
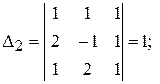
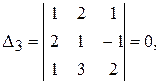
т. о.