 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Группы, кольца, поля
|
|
Будем говорить, что в множестве 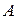 определён закон композиции, если задано отображение
определён закон композиции, если задано отображение  упорядоченных пар элементов из
упорядоченных пар элементов из 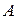 в множество
в множество 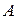 (бинарная операция на множестве
(бинарная операция на множестве 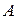 ). При этом элемент
). При этом элемент  из
из 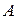 , сопоставленный с помощью отображения
, сопоставленный с помощью отображения  в соответствие элементам
в соответствие элементам  из
из 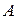 , называется композицией этих элементов.
, называется композицией этих элементов.
Композиция  элементов
элементов 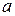 и
и  обозначается символом
обозначается символом  :
:
 .
.
Для композиции элементов  множества
множества 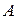 используются и другие формы записи. Наиболее употребительными являются аддитивная форма записи
используются и другие формы записи. Наиболее употребительными являются аддитивная форма записи  и мультипликативная форма записи
и мультипликативная форма записи  (или
(или  ). В случае аддитивной записи композиции соответствующий закон называют сложением, а при мультипликативной форме - умножением.
). В случае аддитивной записи композиции соответствующий закон называют сложением, а при мультипликативной форме - умножением.
Множество 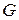 элементов
элементов  , в котором определён закон композиции, называемый сложением и ставящий в соответствие каждой паре элементов
, в котором определён закон композиции, называемый сложением и ставящий в соответствие каждой паре элементов  множества
множества 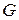 определённый элемент
определённый элемент  этого множества, называется аддитивной группой (обозначается
этого множества, называется аддитивной группой (обозначается  ), если этот закон удовлетворяет следующим требованиям:
), если этот закон удовлетворяет следующим требованиям:
1.  (ассоциативность).
(ассоциативность).
2. Существует элемент  множества
множества 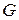 такой, что для любого элемента
такой, что для любого элемента 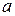 этого множества
этого множества  (существование нейтрального (нулевого) элемента).
(существование нейтрального (нулевого) элемента).
3. Для любого элемента 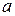 множества
множества 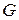 существует противоположный элемент
существует противоположный элемент  такой, что
такой, что 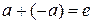 .
.
В случае мультипликативной формы записи получим определение мультипликативной группы (обозначается  ), нейтральный элемент которой называется единичным, а противоположный - обратным
), нейтральный элемент которой называется единичным, а противоположный - обратным  .
.
Если закон композиции, действующий в группе 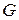 , удовлетворяет следующему требованию:
, удовлетворяет следующему требованию:
4.  (коммутативность),
(коммутативность),
то группа 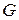 называется коммутативной или абелевой.
называется коммутативной или абелевой.
Отметим некоторые свойства групп (будем использовать аддитивную форму записи композиции).
ТЕОРЕМА 1. Если 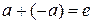 , то
, то  .
.
Доказательство. Пусть  - противоположный элемент для элемента
- противоположный элемент для элемента  :
:  . Тогда
. Тогда  , т. е.
, т. е.  . Следовательно,
. Следовательно,  . Теорема доказана.
. Теорема доказана.
ТЕОРЕМА 2. Для любого элемента 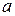 группы справедливо соотношение
группы справедливо соотношение  .
.
ДОКАЗАТЕЛЬСТВО. По теореме 1  и, кроме того,
и, кроме того, 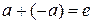 . Поэтому
. Поэтому  , т. е.
, т. е.  . □
. □
ТЕОРЕМА 3. Если  и
и  , то
, то  .
.
ДОКАЗАТЕЛЬСТВО. Так как  , то
, то  - противоположный элемент для
- противоположный элемент для 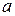 , и поэтому, согласно теореме 1,
, и поэтому, согласно теореме 1,  . Имеем далее
. Имеем далее  . □
. □
Из доказанных теорем вытекают следующие важные следствия.
СЛЕДСТВИЕ 1. Противоположным элементом для элемента  служит элемент
служит элемент 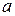 . Или, иначе, элемент
. Или, иначе, элемент  является как правым, так и левым противоположным элементом для элемента
является как правым, так и левым противоположным элементом для элемента 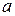 (т. е.
(т. е. 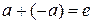 и
и  ).
).
СЛЕДСТВИЕ 2. В любой группе уравнения  и
и  однозначно разрешимы. Решениями этих уравнений служат соответственно элементы
однозначно разрешимы. Решениями этих уравнений служат соответственно элементы  и
и  .
.
СЛЕДСТВИЕ 3. В группе имеется единственный нейтральный элемент (нуль группы)(если  и
и  , то
, то  ).
).
Пример 1. Множество  целых чисел образует абелеву группу относительно сложения. Действительно, сложение целых чисел ассоциативно и коммутативно, нейтральным элементом является целое число
целых чисел образует абелеву группу относительно сложения. Действительно, сложение целых чисел ассоциативно и коммутативно, нейтральным элементом является целое число  , а обратным для
, а обратным для 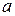 служит целое число
служит целое число  .
.
Пример 2. Множество положительных вещественных чисел 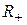 образует абелеву группу относительно умножения. Очевидно, умножение ассоциативно и коммутативно. Нейтральный элемент
образует абелеву группу относительно умножения. Очевидно, умножение ассоциативно и коммутативно. Нейтральный элемент  , а обратным элементом для числа
, а обратным элементом для числа  служит вещественное число
служит вещественное число  .
.
Пример 3. Взаимно однозначное отображение  множества
множества  на себя называется подстановкой из
на себя называется подстановкой из 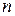 элементов, При этом всякий элемент
элементов, При этом всякий элемент  множества
множества  переходит в элемент
переходит в элемент  , обратная подстановка
, обратная подстановка  переводит
переводит  в
в  . Подстановка
. Подстановка 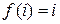 для любого
для любого  множества
множества  называется тождественной подстановкой. Во множестве подстановок
называется тождественной подстановкой. Во множестве подстановок 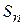 естественным образом определяется закон композиции: если
естественным образом определяется закон композиции: если  и
и  подстановки, то последовательное проведение
подстановки, то последовательное проведение  этих подстановок представляет собой некоторую подстановку. Легко видеть, что композиция ассоциативна. Если множество
этих подстановок представляет собой некоторую подстановку. Легко видеть, что композиция ассоциативна. Если множество 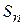 содержит тождественную подстановку, обратную подстановку для каждой своей подстановки
содержит тождественную подстановку, обратную подстановку для каждой своей подстановки  и вместе с любыми двумя подстановками
и вместе с любыми двумя подстановками  и
и  их композицию
их композицию  , то, очевидно,
, то, очевидно, 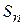 представляет собой группу.
представляет собой группу.
Множество 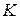 элементов
элементов  , в котором определены законы композиции, называемые сложением и умножением, называется кольцом (обозначается
, в котором определены законы композиции, называемые сложением и умножением, называется кольцом (обозначается  ), если эти законы удовлетворяют следующим требованиям:
), если эти законы удовлетворяют следующим требованиям:
1.  - коммутативная группа.
- коммутативная группа.
2.  (ассоциативность).
(ассоциативность).
3.  и
и  (дистрибутивность умножения относительно сложения).
(дистрибутивность умножения относительно сложения).
Если умножение коммутативно, то кольцо называется коммутативным; если в кольце имеется единичный элемент, то оно называется кольцом с единицей. Элементы  называются делителями нуля - нейтрального элемента относительно
называются делителями нуля - нейтрального элемента относительно  , если
, если 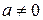 и
и  , но
, но  .
.
Пример 4. Множество целых чисел  относительно сложения и умножения является коммутативным кольцом с единицей. Роль единичного элемента играет целое число
относительно сложения и умножения является коммутативным кольцом с единицей. Роль единичного элемента играет целое число  .
.
Пример 5. Множество квадратных матриц  порядка относительно сложения и умножения образует кольцо с единицей. Коммутативность сложения, ассоциативность сложения и умножения, дистрибутивность умножения относительно сложения для матриц были отмечены в §1.1. Нейтральным элементом по сложению является нулевая квадратная матрица порядка
порядка относительно сложения и умножения образует кольцо с единицей. Коммутативность сложения, ассоциативность сложения и умножения, дистрибутивность умножения относительно сложения для матриц были отмечены в §1.1. Нейтральным элементом по сложению является нулевая квадратная матрица порядка 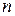 , нейтральным элементом по умножению - единичная матрица порядка
, нейтральным элементом по умножению - единичная матрица порядка 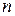 .
.
Коммутативное кольцо с единицей, в котором каждый ненулевой элемент является обратимым, т.е. для любого 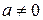 существует
существует  , такой, что
, такой, что  , называется полем.
, называется полем.
ТЕОРЕМА 4. Для любого элемента поля 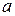 :
:  , где
, где  нейтральный элемент по сложению.
нейтральный элемент по сложению.
ДОКАЗАТЕЛЬСТВО. 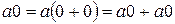 . Таким образом,
. Таким образом,  является нейтральным элементом по сложению, т. е.
является нейтральным элементом по сложению, т. е.  .
.
ТЕОРЕМА 5. В поле нет ненулевых делителей нуля.
ДОКАЗАТЕЛЬСТВО. Если  и
и 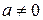 , то существует обратный элемент
, то существует обратный элемент  , обратный к
, обратный к 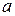 . Тогда
. Тогда 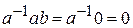 . Но
. Но  . Отсюда
. Отсюда  . □
. □
Пример 6. Множество рациональных чисел  с операциями сложения и умножения образует поле. Действительно, для всякого ненулевого рационального
с операциями сложения и умножения образует поле. Действительно, для всякого ненулевого рационального  , существует так же рациональный обратный элемент
, существует так же рациональный обратный элемент  .
.
Дата публикования: 2014-11-04; Прочитано: 566 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
