Пример 3. Непосредственной проверкой можно убеди

.

Непосредственной проверкой можно убедиться в справедливости следующих свойств операций над матрицами:

1. 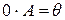- нулевая матрица (все элементы равны ).

2.

3.

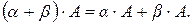
4.

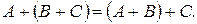
5.

6.

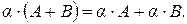
7.

Свойства 4 и 5 называются соответственно ассоциативностью и коммутативностью сложения матриц.

8.

9. .

10.

11.

Свойство 9 носит название ассоциативности умножения, а свойства 10 и 11– дистрибутивности умножения относительно сложения матриц. Эти свойства можно доказать, рассмотрев общий элемент матриц в левой и правой части этого равенства.

12.

Т. е. умножение матриц некоммутативно, например,

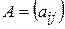Совокупность элементов квадратной матрицы называется главной диагональю. Матрица, у которой элементы, стоящие на главной диагонали, равны единице, а все остальные равны нулю, называется единичной матрицей и обозначается .

.

13. , для любой квадратной матрицы .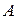

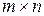Если матрица порядка , а матрица порядка , причём 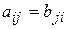, то 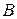называют транспонированной матрицей по отношению к 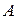и обозначают через

14.

15.

Доказательство свойств 14 и 15 заключается в рассмотрении элемента в правой и левой частях этих равенств. □

Пусть квадратная матрица порядка 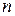. Она называется

- симметрической, если

- кососимметрической, если