 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Теоремы о произведении определителей и обратной матрице. Правило Крамера
|
|
ТЕОРЕМА (о произведении определителей). Определитель произведения двух квадратных матриц 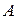 и
и 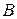 одного и того же порядка равен произведению их определителей, т.е.
одного и того же порядка равен произведению их определителей, т.е. 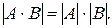
ДОКАЗАТЕЛЬСТВО. Рассмотрим вспомогательный определитель порядка 

Используя теорему Лапласа, вычислим  , разлагая его по первым
, разлагая его по первым 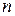 строкам. Так как в них лишь один минор
строкам. Так как в них лишь один минор  может быть не равен
может быть не равен  , а его алгебраическое дополнение есть
, а его алгебраическое дополнение есть  , то
, то  . Используя свойство 9 определителей, добьемся, что все элементы
. Используя свойство 9 определителей, добьемся, что все элементы 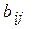 обратились в
обратились в  . Для этого
. Для этого  столбец
столбец  умножим на
умножим на  и прибавим к
и прибавим к  столбцу
столбцу  , и так для каждых
, и так для каждых  и
и  . Получим
. Получим

Вычислим 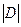 , разлагая его по последним
, разлагая его по последним 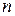 столбцам. Получим
столбцам. Получим  , где
, где  .
.
Тогда  и
и  . Но нетрудно проверить, что
. Но нетрудно проверить, что  . □
. □
Пусть 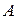 и
и  матрицы порядка
матрицы порядка 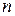 . Матрица
. Матрица 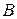 называется обратной для матрицы
называется обратной для матрицы 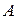 , если
, если  . Матрица
. Матрица 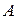 называется невырожденной, если
называется невырожденной, если 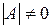 .
.
ЛЕММА (к теореме об обратной матрице).
(а) если  имеет обратную матрицу
имеет обратную матрицу  , то
, то  - невырожденная;
- невырожденная;
(б) если обратная матрица для  существует, то она единственна.
существует, то она единственна.
ДОКАЗАТЕЛЬСТВО.
(а) Имеем 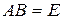 . По теореме о произведении определителей получаем
. По теореме о произведении определителей получаем  . Значит
. Значит 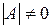 .
.
(б) Пусть  также обратная матрица для
также обратная матрица для 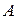 . Используя ассоциативность умножения матриц, имеем
. Используя ассоциативность умножения матриц, имеем  . □
. □
Оказывается утверждение (а) можно обратить.
ТЕОРЕМА (об обратной матрице). Если матрица 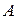 - невырожденная матрица, то она имеет обратную матрицу
- невырожденная матрица, то она имеет обратную матрицу 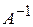 , где
, где
 (4)
(4)
Иными словами,  элемент
элемент 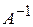 равен алгебраическому дополнению
равен алгебраическому дополнению  элемента
элемента 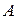 , деленному на
, деленному на  .
.
ДОКАЗАТЕЛЬСТВО. Найдем  элемент произведения матрицы
элемент произведения матрицы 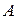 на указанную матрицу
на указанную матрицу 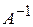 (4). Он равен
(4). Он равен
 .
.
Но по следствиям 1 и 2 из теоремы Лапласа сумма в скобках равна  , если
, если 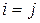 , и равна 0, если
, и равна 0, если  . Следовательно
. Следовательно  . Аналогично, используя замечание после следствия 2, доказывается, что
. Аналогично, используя замечание после следствия 2, доказывается, что 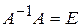 . □
. □
Дата публикования: 2014-11-04; Прочитано: 598 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
