 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Смешанное произведение 2 страница
|
|
6. Найти длину и направление вектора  .
.
7. Какой угол образуют единичные векторы  и
и  , если векторы
, если векторы  и
и  взаимно перпендикулярны?
взаимно перпендикулярны?
8. Даны две точки 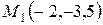 ,
,  . Точка
. Точка  делит отрезок
делит отрезок 
 в отношении
в отношении 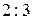 . Найти координаты точки
. Найти координаты точки  .
.
9. На плоскости даны точки  ,
, 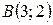 ,
, 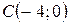 . В начале координат приложены силы
. В начале координат приложены силы  ,
,  и
и  . Найти проекцию вектора
. Найти проекцию вектора  на равнодействующую сил
на равнодействующую сил  .
.
10. Даны координаты вершин треугольника  ,
, 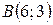 ,
,  . Найти: а) угол
. Найти: а) угол  ; б) площадь треугольника
; б) площадь треугольника  .
.
11. Найти объем пирамиды  , если
, если 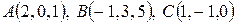 ,
,  .
.
12. Показать, что векторы 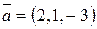 ,
,  ,
,  образуют трехмерный базис и найти координаты вектора
образуют трехмерный базис и найти координаты вектора  в этом базисе.
в этом базисе.
13.  – равнобокая трапеция
– равнобокая трапеция 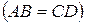 . Каковы могут быть координаты точки
. Каковы могут быть координаты точки  , если известно, что
, если известно, что 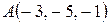 ,
,  ,
, 
ВАРИАНТ 2
1. Даны три матрицы  ,
, 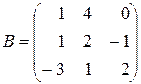 ,
, 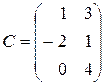 . Найти: а)
. Найти: а)  ; б)
; б)  ; в) ранг матрицы
; в) ранг матрицы 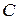 .
.
2. Дана матрица 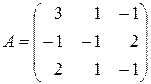 . Найти: а) тремя способами определитель матрицы
. Найти: а) тремя способами определитель матрицы  ; б) матрицу, обратную данной
; б) матрицу, обратную данной  , и сделать проверку.
, и сделать проверку.
3. Показать совместность системы, найти ее решение методами Крамера, Гаусса, обратной матрицы, и сделать проверку
 .
.
4. Даны векторы  ,
,  При каком значении
При каком значении  эти векторы перпендикулярны?
эти векторы перпендикулярны?
5. Найти вектор  , коллинеарный вектору
, коллинеарный вектору 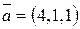 и удовлетворяющий условию
и удовлетворяющий условию  .
.
6. Найти длину и направление вектора  .
.
7. Какой угол образуют единичные векторы  и
и  , если векторы
, если векторы  и
и 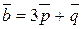 взаимно перпендикулярны?
взаимно перпендикулярны?
8. Даны две точки 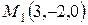 ,
, 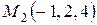 . Точка
. Точка  делит отрезок
делит отрезок 
 в отношении
в отношении 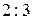 . Найти координаты точки
. Найти координаты точки 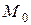 .
.
9. На плоскости даны точки  ,
,  ,
,  . В начале координат приложены силы
. В начале координат приложены силы  ,
,  и
и  . Найти проекцию вектора
. Найти проекцию вектора  на равнодействующую сил
на равнодействующую сил  .
.
10. Даны координаты вершин треугольника  ,
, 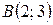 ,
, 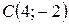 . Найти: а) угол
. Найти: а) угол  ; б) площадь треугольника
; б) площадь треугольника  .
.
11. Найти объем пирамиды  , если
, если  ,
,  .
.
12. Показать, что векторы  ,
,  ,
,  образуют трехмерный базис и найти координаты вектора
образуют трехмерный базис и найти координаты вектора  в этом базисе.
в этом базисе.
13.  – равнобокая трапеция
– равнобокая трапеция 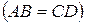 . Каковы могут быть координаты точки
. Каковы могут быть координаты точки  , если известно, что
, если известно, что  ,
,  ,
,  .
.
ВАРИАНТ 3
1. Даны три матрицы  ,
,  ,
,  . Найти: а)
. Найти: а)  ; б)
; б)  ; в) ранг матрицы
; в) ранг матрицы 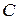 .
.
2. Дана матрица  . Найти: а) тремя способами определитель матрицы
. Найти: а) тремя способами определитель матрицы  ; б) матрицу, обратную данной
; б) матрицу, обратную данной  , и сделать проверку.
, и сделать проверку.
3. Показать совместность системы, найти ее решение методами Крамера, Гаусса, обратной матрицы, и сделать проверку
 .
.
4. Даны векторы  ,
,  При каком значении
При каком значении  эти векторы перпендикулярны?
эти векторы перпендикулярны?
5. Найти вектор  , коллинеарный вектору
, коллинеарный вектору  и удовлетворяющий условию
и удовлетворяющий условию  .
.
6. Найти длину и направление вектора  .
.
7. Какой угол образуют единичные векторы  и
и  , если векторы
, если векторы  и
и  взаимно перпендикулярны?
взаимно перпендикулярны?
8. Даны две точки  ,
,  . Точка
. Точка  делит отрезок
делит отрезок 
 в отношении
в отношении 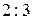 . Найти координаты точки
. Найти координаты точки  .
.
9. На плоскости даны точки  ,
,  ,
,  . В начале координат приложены силы
. В начале координат приложены силы  ,
,  и
и  . Найти проекцию вектора
. Найти проекцию вектора  на равнодействующую сил
на равнодействующую сил  .
.
10. Даны координаты вершин треугольника  ,
,  ,
,  . Найти: а) угол
. Найти: а) угол  ; б) площадь треугольника
; б) площадь треугольника  .
.
11. Найти объем пирамиды  , если
, если  ,
,  .
.
12. Показать, что векторы  ,
,  ,
,  образуют трехмерный базис и найти координаты вектора
образуют трехмерный базис и найти координаты вектора  в этом базисе.
в этом базисе.
13.  – равнобокая трапеция
– равнобокая трапеция 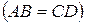 . Каковы могут быть координаты точки
. Каковы могут быть координаты точки  , если известно, что
, если известно, что  ,
, 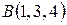 ,
,  .
.
ВАРИАНТ 4
1. Даны три матрицы  ,
,  ,
, 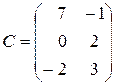 . Найти: а)
. Найти: а)  ; б)
; б)  ; в) ранг матрицы
; в) ранг матрицы 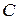 .
.
2. Дана матрица  . Найти: а) тремя способами определитель матрицы
. Найти: а) тремя способами определитель матрицы  ; б) матрицу, обратную данной
; б) матрицу, обратную данной 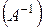 , и сделать проверку.
, и сделать проверку.
3. Показать совместность системы, найти ее решение методами Крамера, Гаусса, обратной матрицы, и сделать проверку
 .
.
4. Даны векторы  ,
,  При каком значении
При каком значении  эти векторы перпендикулярны?
эти векторы перпендикулярны?
5. Найти вектор  , коллинеарный вектору
, коллинеарный вектору 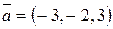 и удовлетворяющий условию
и удовлетворяющий условию 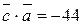 .
.
6. Найти длину и направление вектора  .
.
7. Какой угол образуют единичные векторы  и
и  , если векторы
, если векторы  и
и  взаимно перпендикулярны?
взаимно перпендикулярны?
8. Даны две точки 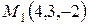 ,
, 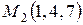 . Точка
. Точка  делит отрезок
делит отрезок 
 в отношении
в отношении 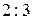 . Найти координаты точки
. Найти координаты точки  .
.
9. На плоскости даны точки  ,
,  ,
,  . В начале координат приложены силы
. В начале координат приложены силы  ,
,  и
и  . Найти проекцию вектора
. Найти проекцию вектора  на равнодействующую сил
на равнодействующую сил  .
.
10. Даны координаты вершин треугольника 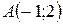 ,
,  ,
, 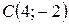 . Найти: а) угол
. Найти: а) угол  ; б) площадь треугольника
; б) площадь треугольника  .
.
11. Найти объем пирамиды  , если
, если  ,
, 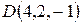 .
.
12. Показать, что векторы  ,
,  ,
, 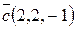 образуют трехмерный базис и найти координаты вектора
образуют трехмерный базис и найти координаты вектора  в этом базисе.
в этом базисе.
13.  – равнобокая трапеция
– равнобокая трапеция 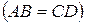 . Каковы могут быть координаты точки
. Каковы могут быть координаты точки  , если известно, что
, если известно, что  ,
,  ,
,  .
.
ВАРИАНТ 5
1. Даны три матрицы  ,
,  ,
, 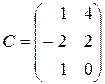 . Найти: а)
. Найти: а)  ; б)
; б)  ; в) ранг матрицы
; в) ранг матрицы 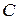 .
.
2. Дана матрица 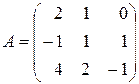 . Найти: а) тремя способами определитель матрицы
. Найти: а) тремя способами определитель матрицы  ; б) матрицу, обратную данной
; б) матрицу, обратную данной 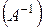 , и сделать проверку.
, и сделать проверку.
3. Показать совместность системы, найти ее решение методами Крамера, Гаусса, обратной матрицы, и сделать проверку
 .
.
4. Даны векторы  ,
,  При каком значении
При каком значении  эти векторы перпендикулярны?
эти векторы перпендикулярны?
5. Найти вектор  , коллинеарный вектору
, коллинеарный вектору  и удовлетворяющий условию
и удовлетворяющий условию  .
.
6. Найти длину и направление вектора  .
.
7. Какой угол образуют единичные векторы  и
и  , если векторы
, если векторы  и
и  взаимно перпендикулярны?
взаимно перпендикулярны?
8. Даны две точки  ,
,  . Точка
. Точка  делит отрезок
делит отрезок 
 в отношении
в отношении 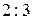 . Найти координаты точки
. Найти координаты точки  .
.
9. На плоскости даны точки  ,
, 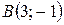 ,
,  . В начале координат приложены силы
. В начале координат приложены силы  ,
,  и
и  . Найти проекцию вектора
. Найти проекцию вектора  на равнодействующую сил
на равнодействующую сил  .
.
10. Даны координаты вершин треугольника 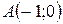 ,
, 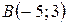 ,
, 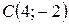 . Найти: а) угол
. Найти: а) угол  ; б) площадь треугольника
; б) площадь треугольника  .
.
11. Найти объем пирамиды  , если
, если 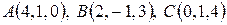 ,
,  .
.
12. Показать, что векторы  ,
,  ,
,  образуют трехмерный базис и найти координаты вектора
образуют трехмерный базис и найти координаты вектора  в этом базисе.
в этом базисе.
13.  – равнобокая трапеция
– равнобокая трапеция 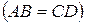 . Каковы могут быть координаты точки
. Каковы могут быть координаты точки  , если известно, что
, если известно, что  ,
,  ,
, 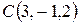 .
.
ВАРИАНТ 6
1. Даны три матрицы  ,
,  ,
,  . Найти: а)
. Найти: а)  ; б)
; б)  ; в) ранг матрицы
; в) ранг матрицы 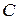 .
.
2. Дана матрица  . Найти: а) тремя способами определитель матрицы
. Найти: а) тремя способами определитель матрицы  ; б) матрицу, обратную данной
; б) матрицу, обратную данной 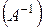 , и сделать проверку.
, и сделать проверку.
3. Показать совместность системы, найти ее решение методами Крамера, Гаусса, обратной матрицы, и сделать проверку
 .
.
4. Даны векторы  ,
,  При каком значении
При каком значении  эти векторы перпендикулярны?
эти векторы перпендикулярны?
5. Найти вектор  , коллинеарный вектору
, коллинеарный вектору  и удовлетворяющий условию
и удовлетворяющий условию  .
.
Дата публикования: 2014-11-04; Прочитано: 655 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
