 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Смешанное произведение 1 страница
|
|
Смешанным произведением трех векторов 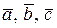 называется скалярное произведение векторного произведения векторов
называется скалярное произведение векторного произведения векторов  и вектора
и вектора  , т.е.
, т.е.
 .
.
Смешанное произведение векторов  ,
,  ,
,  определяется формулой:
определяется формулой:
 .
.
| Теорема. | Смешанное произведение  равно объему параллелепипеда, построенного на векторах равно объему параллелепипеда, построенного на векторах  , ,  и и  , приведенных к общему началу, т.е. , приведенных к общему началу, т.е.
|
 .
.
Замечание. Если векторы  и
и 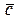 компланарны, то приведя их к общему началу, на них нельзя построить параллелепипед.
компланарны, то приведя их к общему началу, на них нельзя построить параллелепипед.
Необходимым и достаточным условием компланарности трех векторов 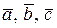 является равенство нулю их смешанного произведения:
является равенство нулю их смешанного произведения:  .
.
Пример 5.1. Показать, что векторы  ,
,  ,
,  являются компланарными.
являются компланарными.
Решение. Необходимым и достаточным условием компланарности трех векторов является соотношение  , т.е. определитель третьего порядка, составленный из координат векторов
, т.е. определитель третьего порядка, составленный из координат векторов  и
и 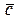 должен равняться нулю. Проверим это:
должен равняться нулю. Проверим это:
 .
.
Определитель равен нулю, т.е. векторы 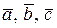 являются компланарными.
являются компланарными.
Пример 5.2. В пространстве даны четыре точки:  ,
,  ,
,  ,
, 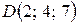 . Найти объем тетраэдра
. Найти объем тетраэдра  .
.
Решение.
Как известно из элементарной геометрии, объем  тетраэдра
тетраэдра  равен одной шестой объема параллелепипеда, построенного на векторах
равен одной шестой объема параллелепипеда, построенного на векторах  ,
,  и
и  . Отсюда заключаем, что
. Отсюда заключаем, что  равняется одной шестой абсолютной величины смешанного произведения
равняется одной шестой абсолютной величины смешанного произведения  .
.
Прежде чем подсчитать смешанное произведение, найдем координаты векторов  ,
,  и
и  :
:
 ,
, 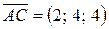 ,
, 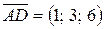 .
.
Тогда
 .
.
Таким образом, объем тетраэдра равен 3 куб.ед.
| III. П р о в е р оч н ы й т е с т |
1. Какая из матриц является транспонированной по отношению к данной матрице  ?
?
а)  ; ;
| б)  ; ;
| в)  ; ;
| г)  . .
|
2. Какая из данных матриц является диагональной?
а)  ; ;
| б)  ; ;
| в)  ; ;
| г)  . .
|
3. Какая из представленных матриц является единичной?
а) 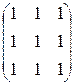 ; ;
| б)  ; ;
| в)  ; ;
| г)  . .
|
4. Для каких из представленных матриц определена операция умножения?
а)  ; ;
| б)  ; ;
|
в)  ; ;
| г) 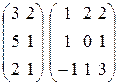 . .
|
5. Какой будет размерность матрицы С, полученной в результате умножения матриц А размерностью (5  6), и В размерностью (6
6), и В размерностью (6  4)?
4)?
а) (5  6); б) (6
6); б) (6  4); в) (6
4); в) (6  6); г) (5
6); г) (5  4).
4).
6. Какая из приведенных матриц является суммой матриц 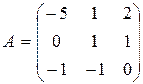 и
и 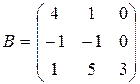 ?
?
а)  ; ;
| б)  ; ;
| в)  ; ;
| г)  . .
|
7. Какая матрица получится в результате умножения матрицы 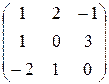 на число 4?
на число 4?
а)  ; ;
| б)  ; ;
| в)  ; ;
| г)  . .
|
8. Какая из представленных матриц является произведением матриц  и
и  ?
?
а)  ; ;
| б)  ; ;
| в)  ; ;
| г)  . .
|
9. Не вычисляя, ответьте, какое из перечисленных ниже равенств является верным?
| а) |    ; ;
|
| б) |  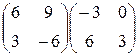 ; ;
|
| в) |   ; ;
|
| г) |  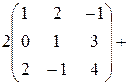  . .
|
10. Пусть  . Какое из перечисленных ниже равенств не является верным?
. Какое из перечисленных ниже равенств не является верным?
а)  ; ;
| б) 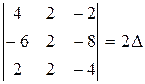 ; ;
|
в)  ; ;
| г) 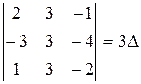 . .
|
11. Не вычисляя, указать какой из определителей не равен нулю
а)  ; ;
| б)  ; ;
| в)  ; ;
| г)  . .
|
12. В каком случае значение определителя не изменится?
а) если поменять местами две строки;
б) если поменять местами все строки и столбцы;
в) если поменять местами два столбца;
г) если один из столбцов умножить на (– 2).
13. Какое из перечисленных ниже равенств не является верным?
а)  ; ;
| б)  ; ;
|
в)  ; ;
| г)  . .
|
14. Определить ранг матрицы  .
.
| а) 4 | б) 3 | в) 2 | г) 1 |
15. Даны два вектора  ,
, 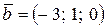 . Каковы будут координаты вектора
. Каковы будут координаты вектора  ?
?
а) 
| б) 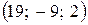
| в) 
| г) 
|
16. Какой из представленных векторов является коллинеарным вектору  ?
?
а) 
| б) 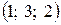
| в) 
| г) 
|
17. Какой из векторов образует с вектором  угол в 90о?
угол в 90о?
а) 
| б) 
| в) 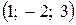
| г) 
|
18. Определить длину вектора 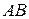 , если
, если  и
и  .
.
а) 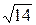
| б) 
| в) 
| г) 
|
19. Какая из представленных точек является симметричной точке (2; 3) относительно оси абсцисс?
а) 
| б) 
| в) 
| г) 
|
20. Какая из представленных точек является симметричной точке  относительно оси ординат?
относительно оси ординат?
а) 
| б) 
| в) 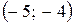
| г) 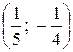
|
21. Какая из представленных точек является симметричной точке 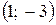 относительно начала координат?
относительно начала координат?
а) 
| б) 
| в) 
| г) 
|
22. Найдите проекцию вектора 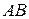 на ось абсцисс, если
на ось абсцисс, если  ,
,  .
.
| а) – 3 | б) 0 | в) 3 | г) 
|
23. Найдите угол между векторами  и
и 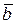 , если
, если  ,
,  .
.
| а) 45о | б) 
| в) 
| г) 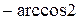
|
24. Даны векторы 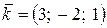 ,
, 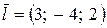 ,
,  ,
, 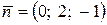 . Какое из приведенных ниже равенств не является верным?
. Какое из приведенных ниже равенств не является верным?
а) 
| б) 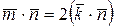
|
в) 
| г) 
|
25. Какая из приведенных ниже формул верна
а) 
| б) 
|
в) 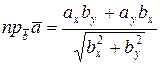
| г) 
|
26. Векторным произведением вектора  на вектор
на вектор 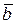 называется вектор
называется вектор  , который удовлетворяет следующим условиям…
, который удовлетворяет следующим условиям…
Продолжите предложение, указав какое из приведенных ниже положений лишнее
| а) | длина вектора  равна произведению длин векторов равна произведению длин векторов  и и 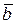 на синус угла на синус угла  между ними: между ними: 
|
| б) | вектор  перпендикулярен векторам перпендикулярен векторам  и и 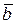
|
| в) | вектор  ни при каких значениях векторов ни при каких значениях векторов  и и 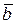 не должен обращаться в ноль не должен обращаться в ноль
|
| г) | вектор  направлен таким образом, что кратчайший поворот от направлен таким образом, что кратчайший поворот от  к к 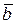 виде из его конца совершающимся против часовой стрелки. виде из его конца совершающимся против часовой стрелки.
|
27. На плоскости даны точки  ,
,  ,
,  . В начале координат приложены силы
. В начале координат приложены силы 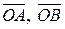 и
и  . Найти равнодействующую сил
. Найти равнодействующую сил  .
.
а) 
| б) 
| в) 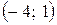
| г) 
|
28. Какая из представленных ниже формул не верна для нахождения площади треугольника, построенном на векторах  и
и 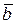 (
( – угол между векторами).
– угол между векторами).
а) 
| б) 
| в) 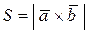
| г) 
|
29. Найти скалярное произведение единичных векторов  и
и  , которые образуют между собой угол в 60о.
, которые образуют между собой угол в 60о.
| а) 1 | б) 
| в) 
| г) 2 |
30. Найдите направляющие косинусы вектора 
а) 
| б) 
| в) 
| г) 
|
31. При каком значении  векторы
векторы  ,
,  ,
,  являются компланарными?
являются компланарными?
| а) – 2 | б) 
| в) 4 | г) – 1 |
Ответы и указания к тесту смотрите на стр. 78
| IV и н д и в и д у а л ь н ы е з а д а н и я |
ВАРИАНТ 1
1. Даны три матрицы  ,
, 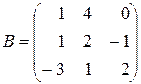 ,
,  . Найти: а)
. Найти: а) 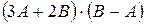 ; б)
; б)  ; в) ранг матрицы
; в) ранг матрицы 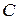 .
.
2. Дана матрица  . Найти: а) тремя способами определитель матрицы
. Найти: а) тремя способами определитель матрицы  ; б) матрицу, обратную данной
; б) матрицу, обратную данной 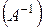 , и сделать проверку.
, и сделать проверку.
3. Показать совместность системы, найти ее решение методами Крамера, Гаусса, обратной матрицы, и сделать проверку
 .
.
4. Даны векторы  ,
,  При каком значении
При каком значении  эти векторы перпендикулярны?
эти векторы перпендикулярны?
5. Найти вектор  , коллинеарный вектору
, коллинеарный вектору  и удовлетворяющий условию
и удовлетворяющий условию  .
.
Дата публикования: 2014-11-04; Прочитано: 694 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
