Уравнения прямой на плоскости

Уравнение прямой с угловым коэффициентом

a

a

y

x

x ¢

x

y

O

M (x; y)

N (0; b)

Рис. 21

K (x; b)

Пусть прямая пересекает ось Oy в точке N (0; b) и образует с осью Ox угол a (0 £ a < p) (Рис. 21). Возьмем на прямой произвольную точку M (x; y). Тогда тангенс угла a наклона прямой найдем изпрямоугольного треугольника MNK:

.

Введем обозначение , получаем уравнение

y = kx + b, (3.5)

которому удовлетворяют координаты любой точки M (x; y) прямой.

Число называется угловым коэффициентом прямой, а уравне­ние (3.1) - уравнением прямой с угловым коэффициентом.

Если прямая параллельна оси Oy, то , уравнение (3.5) теряет смысл, т. к. для нее угловой коэффициент не существует. В этом случае уравнение прямой имеет вид х = а, где а - абсцисса точки пересечения прямой с осью Ox.

Общее уравнение прямой

Определение. Любая прямая на плоскости может быть задана уравнением первого порядка

Ах + Ву + С = 0, (3.6)

где А, В, С - произвольные числа, причем А, В не равны нулю одновременно, т. е. А ² + В ² ¹ 0. Это уравнение первого порядка называют общим уравнением прямой.

В зависимости от значений постоянных А, В и С возможны следующие частные случаи:

· C = 0, А ¹ 0, В ¹ 0 – прямая проходит через начало координат;

· А = 0, В ¹ 0, С ¹ 0 (By + C = 0) - прямая параллельна оси Ох;

· В = 0, А ¹ 0, С ¹ 0 (A x + C = 0) – прямая параллельна оси Оу;

· В = С = 0, А ¹ 0 – прямая совпадает с осью Оу;

· А = С = 0, В ¹ 0 – прямая совпадает с осью Ох.

Уравнение прямой, проходящей через данную точку в данном направлении

Пусть прямая проходит через точку M (x ₀; y ₀) и образует с осью Ох угол . Уравнение этой прямой можно записать в виде y ₀ = kx ₀ + b. Отсюда b = y ₀ - kx ₀. Подставляя значение b в уравнение (3.1), получим искомое уравнение прямой y = kx + y ₀ - kx ₀, т. е.

y - y ₀ = k (x - x ₀). (3.7)

Уравнение (3.7) с различными значениями k называют уравнениями пучка прямых с центром в точке M (x ₀; y ₀). Из этого уравнения нельзя определить лишь прямую, параллельную оси Oy.

Пример 3. Составить уравнение прямой, проходящей через точ­ку (2; -4) и имеющей угловой коэффициент k = 3.

Решение. Точку (2; -4) обозначим М ₀, тогда на основании урав-нения пучка прямых (3.7) имеем y - (-4) = 3(x - 2), или 3 x - y - 10 = 0.

Уравнение прямой, проходящей через две точки

Пусть заданы две точки M ₁(x ₁; y ₁), M ₂(x ₂; y ₂) и х ₁ ¹ х ₂, y ₁ ¹ y ₂. Для составления уравнения прямой М ₁ М ₂ запишем уравнение пучка прямых, про­ходящих через точку М ₁: y - y ₁ = k (x - x ₁). Т. к. прямая проходит через точку М ₂, то координаты этой точки должны удовлетворять уравнению пучка прямых: y ₂ - y ₁ = k (x ₂ - x ₁). Отсюда находим угловой коэффициент

.

Тогда уравнение прямой, проходящей через эти точки имеет вид

,

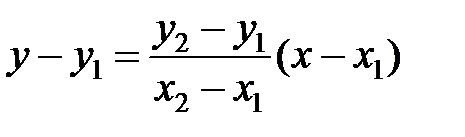или

. (3.8)

Если какой-либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель.

Пример 4. Найти уравнение прямой, проходящей через точки А (1; 2) и В (3; 4).

Решение. Применяя формулу (3.8), получаем

или .

Уравнение прямой в отрезках

Если в общем уравнении прямой (3.6) С ¹ 0, то, разделив на – С, полу­чим: или

, (3.9)

где

.

a

b

O

y

x

M 1(0; b)

M 2(a;0)

Рис. 22

Уравнение вида (3.9) называется уравнением пря­мой в отрезках. Геометрический смысл коэффициентов в том, что коэффициент а является абсциссой точки пересечения прямой с осью Ох, а b – ордината точки пересечения прямой с осью Оу (рис. 23).

Пример 5. Задано общее уравнение прямой х – у + 1 = 0. Найти уравнение этой прямой в отрезках.

Решение. Определим коэффициенты a и b

Составим искомое уравнение прямой в отрезках вида (3.9)

.

Пример 6. Прямая отсекает на координатных осях равные положительные отрезки. Составить уравнение прямой, если площадь треуголь­ника, образованного этими отрезками равна 8 см².

Решение. Уравнение прямой имеет вид (3.9). Определим коэф­фициенты a и b. Согласно условию a = b, S _D = ab /2 = 8 Þ a = b = ±4, a = -4 не подходит по условию задачи.

Подставляем найденные значения a и b в формулу (3.9)

или х + у – 4 = 0.

Уравнение прямой, проходящей через заданную точку перпендикулярно данному вектору

Найдем уравнение прямой, проходящей через заданную точку M ₀(x ₀; y ₀) перпендикулярно данному ненулевому вектору (рис. 24).

O

y

x

M 0(x 0; y 0)

M (x; y)

Рис. 23

Возьмем на прямой произвольную точку M (x; y) и рассмотрим вектор . Поскольку , то их скалярное произведение равно нулю: , т. е.

A (x - x ₀) + B (y - y ₀) = 0. (3.10)

Уравнение (3.10) называется уравнением прямой, проходящей через заданную точку перпендикулярно данному вектору.

Вектор , перпендикулярный прямой, называется нормаль­ным вектором этой прямой.

Пример 7. Найти уравнение прямой, проходящей через точку А (1; 2) перпендикулярно вектору (3; -1).

Решение. Составим при А = 3 и В = -1 общее уравнение прямой: 3 х – у + С = 0. Для нахождения коэффициента С подставим в полученное выражение координаты заданной точки А. Получаем: 3 – 2 + C = 0, следо­вательно С = -1.

Итак, искомое уравнение: 3 х – у – 1 = 0.

Нормальное уравнение прямой

Если обе части общего уравнения прямой Ах + Ву + С = 0 разделить на число , которое называется нормирующем множителем, то получим

х cosj + y sinj - p = 0, (3.11)

O

y

x

Рис. 24

р

j

где р – длина перпендикуляра, опущенного из начала координат на прямую, а j - угол, образованный этим перпендикуляром с положительным направлением оси Ох (рис. 25).

Уравнение вида (3.11) называется нормальным уравнением прямой.

Знак ± нормирующего множителя выбирается из условия m×С < 0.

Пример8. Дано общее уравнение прямой 12 х – 5 у – 65 = 0. Требуется написать различные типы уравнений этой прямой.

- уравнение этой прямой в отрезках:

- уравнение этой прямой с угловым коэффициентом: (делим на 5)

- нормальное уравнение прямой:

;

cos j = 12/13; sin j = -5/13; p = 5.

Следует отметить, что не каждую прямую можно представить уравнением в отрезках, например, прямые, параллельные осям или проходящие через начало координат.