Окружность

Определение. Окружностью радиуса R с центром в точке М ₀ называется множество всех точек М плоскости, удовлетворяющих условию М ₀ М = R (Рис. 27).

Из условия М ₀ М = R получаем уравнение , т. е.

(x – x ₀)² + (y – y ₀)² = R ². (3.15)

O

y

x

М 0(x 0, y 0)

М (x, y)

Рис. 27

R

Уравнение (3.15) называется каноническим уравнением окружности. В частности, если x ₀ = y ₀ = 0, то имеем уравнение окружности с центром в начале координат x ² + y ² = R ². Если R = 0, то уравнению (3.15) удовлетворяют координаты единственной точки М ₀(x ₀, y ₀) и говорят, что «окружность выродилась в точку».

Пример12. Найти координаты центра и радиус окружности, если ее уравнение задано в виде

2 x ² + 2 y ² – 8 x + 5 y – 4 = 0.

Решение. Для нахождения координат центра и радиуса окружности данное уравнение необходимо привести к виду (3.15). Для этого выделим полные квадраты

x ² + y ² – 4 x + 2,5 y – 2 = 0,

x ² – 4 x + 4 – 4 + y ² + 2,5 y + 25/16 – 25/16 – 2 = 0,

(x – 2)² + (y + 5/4)² = 121/16.

Отсюда находим М ₀(2; -5/4), R = 11/4.

Эллипс

Рис. 28

y

M

b

a

x

r 1

F 1

F 2

r 2

с

O

А 1

А 2

В 1

В 2

Определение. Эллипсом называется множество всех точек М плоскости, сумма расстояний от каждой из которых до двух данных точек этой плоскости F ₁ и F ₂, называемых фокусами, есть величина постоянная равная 2 а, большая, чем расстояние между фокусами (Рис. 28).

Выберем фокусы так, чтобы они лежа­ли на оси Ох, а начало координат совпадало с серединой отрезка F ₁ F ₂, тогда фокусы имеют координаты F ₁(- c, 0), F ₂(c, 0), значит расстояние между ними равно 2 с. По определению 2 а > 2 c, т. е. a > c.

Пусть M (x, y) - произвольная точка эллипса. Тогда, по определению эллипса, MF ₁ + MF ₂ = 2 a, т. е.

,

.

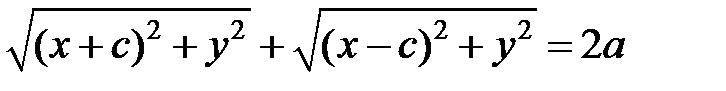Возведем полученное уравнение в квадрат и приведем подобные

,

.

Т. к. a > c, то a ² - c ² > 0. Положим a ² - c ² = b ². Тогда последнее уравнение примет вид или

. (3.16)

Уравнение (3.16) называется каноническим уравнением эллипса. Эллипс пересекает координатные оси в точках А ₁(a,0), А ₂(- a,0), В ₁(0, b), В ₂(0,- b), которые называются вершинами эллипса. Отрезки А ₁ А ₂ и В ₁ В ₂, равные 2 a и 2 b, соответственно называются большой и малой осями эллипса, a и b – большой и малой полуосями.

Определение. Форма эллипса определяется характеристикой, которая является отношением половины расстояния между фокусами к большей оси и называется эксцентриситетом

e = с / a.

Т. к. 0 < с < a, то 0 < e < 1.

Чем больше эксцентриситет, тем более вытянутую форму вдоль оси Ox имеет кривая.

Теорема3.3. Для произвольной точки М (х, у), принадлежащей эллипсу верны соотношения для фокальных радиусов r ₁ и r ₂ точки

r ₁ = a + e x, r ₂ = a - e x.

Доказательство. Из определения эллипса следует, что r ₁ + r ₂ = 2 a. Кроме того, из геометрических соображений можно записать

После возведения в квадрат и приведения подобных слагаемых

Аналогично доказывается, что r ₁ = a + e x. Теорема доказана.

С эллипсом связаны две прямые, называемые директрисами. Их уравнения

x = a /e, x = - a /e.

r

F 1

F 2

y

x

d

x = - a /e

x = a /e

Рис. 29

Теорема 3.4. Если r - расстояние от произвольной точки эллипса до какого-нибудь фокуса, d - расстояние от этой же точки до соответствующей этому фокусу директрисы, то отношение r/d есть постоянная величина, равная эксцентриситету эллипса: (рис. 30).

Пример 13. Составить уравнение пря­мой, проходящей через левый фокус и нижнюю вершину эллипса, задан­ного уравнением:

Решение.

1) Координаты нижней вершины В ₂: x = 0, y ² = 16, y = -4; В ₂(0;-4).

2) Координаты левого фокуса F ₁: c ² = a ² – b ² = 25 – 16 = 9; c = 3; F ₁(-3;0).

3) Уравнение прямой, проходящей через две точки:

Пример 14. Составить уравнение эллипса, если его фокусы F ₁(0; 0), F ₂(1; 1), большая ось равна 2.

Решение. Расстояние между фокусами

2 c = 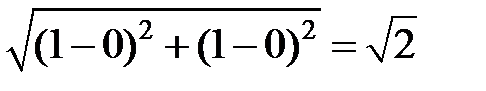, таким образом, a ² – b ² = c ² = ½.

По условию 2 а = 2, следовательно,

а = 1, b ² =

Значит искомое уравнение эллипса .