Частные производные функции двух переменных

Определение. Число 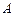называется пределом функции двух переменных в точке , если для любого положительного числа существует положительное число , зависящее от 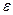, такое что для всех точек отстоящих от точки на расстоянии выполняется неравенство . Обозначение: .

Рассмотрим изменение функции при изменении только одной переменной, например, 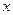; при этом другая переменная 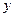остается фиксированной

- частное приращение функции 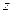по переменной 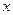. Аналогично определяется частное приращение функции 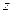по переменной : .

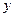Определение. Частной производной функции двух переменных по одной из этих переменных называется предел отношения соответствующего частного приращения функции к приращению рассматриваемой независимой переменной при стремлении последнего к нулю (если этот предел существует).

Пусть , тогда , .

Замечание. Так как частная производная функции 2-х переменных представляет собой обыкновенную производную функции одной переменной при постоянном значении другой переменной, то вычисляют частные производные по формулам и правилам дифференцирования функции одной переменной.

Пример. Найти частные производные функций а) , б) .

Решение. а) , . б) , .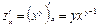

Правило. Производная вычисляется при фиксированном значении 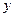, а производная вычисляется при фиксированном значении .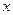

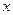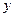Определение. Пусть функция имеет частные производные и , которые также являются функциями двух переменных и . Частные производные от этих функций называются частными производными второго порядка от функции . Каждая производная первого порядка имеет две частные производные. Таким образом, мы получаем 4 частные производные второго порядка, которые обозначаются следующим образом:

,	,
,	.

Определение. 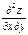и называются смешанными производными функции .