Достаточные признаки существования экстремума (доказать одну из теорем)

Теорема (первое достаточное условие экстремума). Пусть в точке 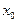функция 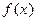непрерывна, а производная 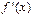при переходе через точку 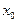меняет знак. Тогда 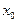– точка экстремума: максимума, если знак меняется с «+» на «–», и минимума, если с «–» на «+».

Доказательство. Пусть при и при .

По теореме Лагранжа , где .Тогда если , то ; поэтому и 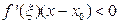, следовательно, , или . Если же , то ; поэтому и , следовательно, или .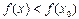

Таким образом доказано, что в любых точках вблизи 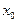, т.е. 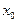– точка максимума функции .

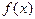Доказательство теоремы для точки минимума проводится аналогично. Теорема доказана.

Если при переходе через точку 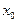производная не меняет знак, то в точке 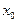экстремума нет.

Теорема (второе достаточное условие экстремума). Пусть в точке 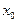производная дважды дифференцируемой функции 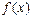равна 0 (), а ее вторая производная в этой точке отлична от нуля () и непрерывна в некоторой окрестности точки 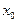. Тогда 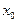– точка экстремума 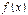; при это точка минимума, а при это точка максимума.