 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Алгоритм нахождения экстремумов функции с помощью второго достаточного условия экстремума
|
|
1. Найти производную 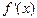 .
.
2. Найти вторую производную  .
.
3. Найти те точки, в которых  .
.
4. В этих точках определить знак  .
.
5. Сделать вывод о существовании и характере экстремумов.
6. Найти экстремальные значения функции.
Пример. Рассмотрим  . Найдем
. Найдем  . Далее,
. Далее,  при
при  и при
и при 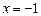 . Исследуем критические точки с помощью первого достаточного условия экстремума. Имеем, что
. Исследуем критические точки с помощью первого достаточного условия экстремума. Имеем, что  при
при  и при
и при  , и
, и 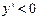 при
при  . В точках
. В точках  и
и  производная меняет свой знак: при
производная меняет свой знак: при  с «+» на «–» и при
с «+» на «–» и при  с «–» на «+». Это значит, что в точке
с «–» на «+». Это значит, что в точке 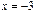 функция имеет максимум, а точке
функция имеет максимум, а точке 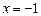 – минимум;
– минимум;  . Для сравнения исследуем критические точки с помощью второго достаточного условия экстремума. Найдем вторую производную
. Для сравнения исследуем критические точки с помощью второго достаточного условия экстремума. Найдем вторую производную 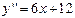 . Имеем:
. Имеем:  , а это значит, что в точке
, а это значит, что в точке  функция имеет максимум, а точке
функция имеет максимум, а точке  – минимум.
– минимум.
Дата публикования: 2014-11-04; Прочитано: 437 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
