Понятие асимптоты графика функции. Горизонтальные, наклонные и вертикальные асимтоты. Примеры

Определение. Асимптотой графика функции называется прямая, обладающая тем свойством, что расстояние от точки до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.

Различают вертикальные (рис. 6.6 а), горизонтальные (рис. 6.6 б) и наклонные (рис. 6.6 в) асимптоты.

На рис. 6.6а изображена вертикальная асимптота.

На рис 6.6б – горизонтальная асимптота.

На рис. 6.6в – наклонная асимптота.

Теорема 1. В точках вертикальных асимптот (например, ) функция 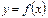терпит разрыв, ее предел слева и справа от точки равен :

и (или) .

Теорема 2. Пусть функция 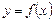определена при достаточно больших 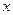и существуют конечные пределы

и .

Тогда прямая является наклонной асимптотой графика функции .

Теорема 3. Пусть функция определена при достаточно больших 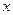и существует предел функции . Тогда прямая есть горизонтальная асимптота графика функции .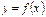

Горизонтальная асимптота является частным случаем наклонной асимптоты, когда . Поэтому, если в каком-либо направлении кривая имеет горизонтальную асимптоту, то в этом направлении нет наклонной, и наоборот.

Пример. Найти асимптоты графика функции .

Решение. В точке функция не определена, найдем пределы функции слева и справа от точки :

; .

Следовательно, - вертикальная асимптота.

Найдем наклонную асимптоту: ; . Таким образом, - наклонная асимптота (рис. 6.7).