 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Формулы производных основных элементарных функций (одну из формул вывести). Производная сложной функции
|
|
Производные основных элементарных функций (таблица производных)
1. Производная логарифмической функции.
А) 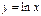 . Воспользуемся схемой нахождения производных:
. Воспользуемся схемой нахождения производных:
1) Дадим аргументу приращение 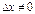 и найдем наращение значений функции
и найдем наращение значений функции 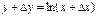 .
.
2) Находим приращение функции 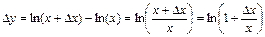 .
.
3) Составляем отношение 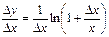 .
.
4) Находим предел этого отношения при 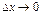 , т.е.
, т.е. 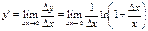 .
.
Обозначив 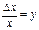 , найдем
, найдем 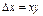 и
и 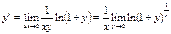 .
.
В силу непрерывности логарифмической функции, используя 3 свойство функций непрерывных в точке. (Если функция 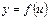 непрерывна в точке
непрерывна в точке 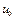 , а функция
, а функция 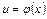 непрерывна в точке
непрерывна в точке 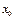 , то сложная функция
, то сложная функция 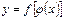 непрерывна в точке
непрерывна в точке 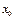 -
- 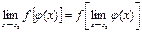 ), меняем местами символы предела и логарифма, а затем используем определение числа
), меняем местами символы предела и логарифма, а затем используем определение числа 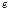 ; получим:
; получим:
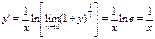 .
.
Итак, 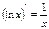 и
и 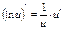 .
.
Б) 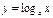 . Найдем
. Найдем 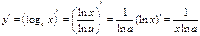 , т.е.
, т.е.
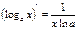 и
и 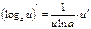 .
.
2. Производная показательной функции.
А) 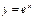 - прологарифмируем обе части равенства по основанию
- прологарифмируем обе части равенства по основанию 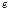 :
: 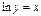 . Дифференцируем
. Дифференцируем 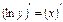 или
или 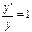 , откуда
, откуда 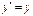 , т.е.
, т.е.
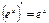 и
и 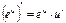 .
.
Б) 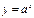 .
. 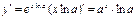 . Итак,
. Итак,
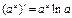 и
и 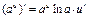
3. Производная степенной функции.
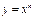 , для любого
, для любого 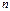 . Прологарифмируем обе части равенства
. Прологарифмируем обе части равенства 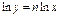 . Дифференцируем:
. Дифференцируем: 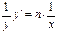 , откуда
, откуда 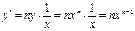 , т.е:
, т.е:
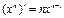 и
и 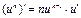
4. Производная степенно-показательной функции.
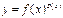 .
. 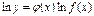 . Дифференцируем:
. Дифференцируем: 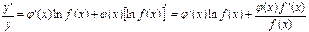 .
.
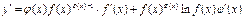
5. Производная тригонометрических функций.
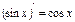 и
и 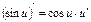
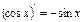 и
и 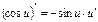
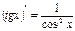 и
и 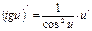
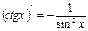 и
и 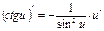
Дата публикования: 2014-11-04; Прочитано: 473 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
