 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Уравнение прямой на плоскости
|
|
В декартовой системе координат рассмотрим прямую 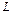 , расположенную под углом
, расположенную под углом 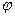 к оси
к оси 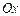 (рис. 3.7).
(рис. 3.7).

| Выберем на прямой L произвольную точку  . Из . Из 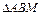 найдем тангенс угла наклона прямой: найдем тангенс угла наклона прямой: 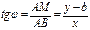 .
Введем угловой коэффициент прямой .
Введем угловой коэффициент прямой 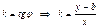 .
Из последнего равенства .
Из последнего равенства 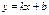 (3.1) (3.1)
|
Полученное уравнение называется уравнением прямой с угловым коэффициентом.
Частные случаи уравнения (3.1):
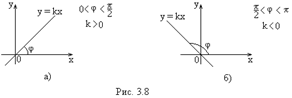
1) Если 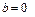 , тогда
, тогда 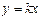 и уравнение (3.1) представляет прямую, проходящую через начало координат под углом
и уравнение (3.1) представляет прямую, проходящую через начало координат под углом 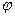 к оси
к оси 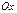 (рис. 3.8).
(рис. 3.8).

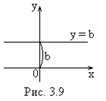
2) Если 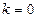 (т.е.
(т.е. 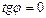 ), тогда
), тогда 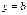 и уравнение (3.1) представляет собой прямую, параллельную оси
и уравнение (3.1) представляет собой прямую, параллельную оси  (рис. 3.9).
(рис. 3.9).
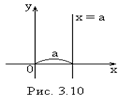

3) Если 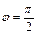 , тогда прямая
, тогда прямая 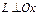 (рис. 3.10). Предположим, что
(рис. 3.10). Предположим, что 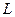 отсекает на оси
отсекает на оси 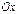 отрезок, равный
отрезок, равный 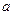 (рис. 3.10). Очевидно, что уравнений такой прямой
(рис. 3.10). Очевидно, что уравнений такой прямой  .
.
Дата публикования: 2014-11-04; Прочитано: 333 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
