Рассмотрим частные случаи уравнения (3.6)

1) Пусть . Тогда уравнение можно записать в виде: . Обозначим .

Если 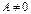, , 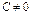то получим (уравнение прямой с угловым коэффициентом);

Если 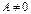, , то (уравнение прямой, проходящей через начало координат);

Если , , 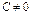то (уравнение прямой, параллельной оси Оу);

Если , , то 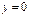(уравнение оси Ох).

3) Пусть , 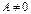. Тогда уравнение примет вид . Обозначим .

Если 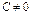, то получим (уравнение прямой, параллельной оси Оу);

Если , то (уравнение оси Оу).

Т.о., при любых значениях коэффициентов 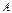, 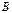(не равных одновременно нулю) и уравнение есть уравнение некоторой прямой линии на плоскости Оху.

- общее уравнение прямой.

Условия параллельности и перпендикулярности двух прямых:

Если прямые и параллельны, то угол и , откуда из формулы угла между двумя прямыми . И наоборот, если , то по этой же формуле и .

Т.о., равенство угловых коэффициентов является необходимым и достаточным условием параллельности 2х прямых.

- условие параллельности двух прямых.

Если прямые перпендикулярны, то , при этом или , откуда или .

Справедливо так же и обратное утверждение.

Т.о., для перпендикулярности прямых необходимо и достаточно, чтобы их угловые коэффициенты были обратны по величине и противоположны по знаку.

- условие перпендикулярности двух прямых.

Если две прямые заданы уравнениями в общем виде: и ,то учитывая их угловые коэффициенты 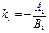и , условие параллельности прямых имеет вид: .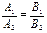

Следовательно, условием параллельности прямых, заданных общими уравнениями является пропорциональность коэффициентов при переменных.

Условие перпендикулярности прямых в этом случае примет вид или ,

Т.е. условием перпендикулярности двух прямых, заданных общими уравнениями, является равенство нулю суммы произведений коэффициентов при переменных х и у.