Уравнение оси ;

Рис. 9

Для того, чтобы построить прямую, достаточно взять две точки: , т.е. прямая проходит через точки (0;4) и (-4;0). Прямая проходит через точки (0;7) и (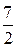;0).

Итак, мы получили многоугольник . Координаты вершин мы знаем, а координаты вершины 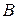найдем, решая систему

:

т.е.

Вычислим значения функции 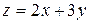в полученных вершинах многоугольника:

n

3.2 Прямая в пространстве

Пусть заданы вектор и точка (рис. 10)

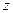
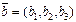
Рис. 10

Параметрические уравнения прямой, проходящей через точку в направлении вектора имеют вид:

(3.4)

Здесь 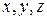- координаты текущей точки 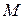прямой, а 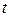- параметр, принимающий все значения от - до 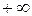. При этом существует взаимно однозначное соответствие между значениями 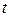и точками прямой. Вектор называют направляющим (или базисным) вектором прямой.

Иногда используют также канонические уравнения прямой:

.

Пример 11. (Образец выполнения задачи 7(a) из контрольной работы). Составить канонические и параметрические уравнения прямой, проходящей через две данные точки и .

Решение. В качестве направляющего возьмем вектор (рис. 11),

Рис. 11

а в качестве фиксированной точки – точку и запишем искомые параметрические уравнения

Канонические уравнения данной прямой будут иметь вид:

.n

Пример 12. При каких и прямые

и

параллельны? Составить уравнение прямой, параллельной данным и проходящей через точку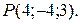

Решение. Прямые параллельны тогда и только тогда, когда их направляющие векторы и коллинеарны, т.е. их соответствующие координаты пропорциональны

,

откуда Прямая, параллельная данным и проходящая через точку , имеет тот же направляющий вектор (3;-2;-1); ее параметрические уравнения таковы

, . n