 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Линейная зависимость и линейная независимость системы векторов
|
|
Вектор 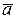 называется линейной комбинацией векторов
называется линейной комбинацией векторов  , если найдутся действительные числа
, если найдутся действительные числа  такие, что:
такие, что:
.
Система векторов называется линейно зависимой, если хотя бы один из векторов системы является линейной комбинацией остальных.
Если ни один из векторов системы не представляется как линейная комбинация других, то система называется линейно независимой.
Линейная зависимость векторов в  означает их коллинеарность (параллельность). Любая пара неколлинеарных векторов является линейно независимой.
означает их коллинеарность (параллельность). Любая пара неколлинеарных векторов является линейно независимой.
Линейная зависимость трех векторов в  означает их компланарность (принадлежность одной плоскости).
означает их компланарность (принадлежность одной плоскости).
Теорема 1. Система векторов 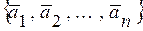 – линейно независима в
– линейно независима в  тогда и только тогда, когда уравнение:
тогда и только тогда, когда уравнение:

имеет только тривиальное решение, т.е. 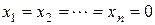 . Система линейно зависима тогда и только тогда, когда данное уравнение имеет не тривиальное решение, т.е.
. Система линейно зависима тогда и только тогда, когда данное уравнение имеет не тривиальное решение, т.е.  .
.
Теорема 2. (Критерий линейной зависимости (независимости) системы из двух векторов).
Два вектора 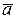 и
и 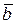 линейно зависимы (линейно независимы) тогда и только тогда, когда все их соответствующие координаты пропорциональны (непропорциональны).
линейно зависимы (линейно независимы) тогда и только тогда, когда все их соответствующие координаты пропорциональны (непропорциональны).
Пример 1. Выяснить, являются ли линейно зависимыми векторы  и
и  .
.
Решение. Определим, пропорциональны ли координаты векторов:
 – верно.
– верно.
Следовательно, векторы 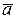 и
и 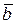 линейно зависимы. n
линейно зависимы. n
Теорема 3. (Критерий линейной зависимости (независимости) системы из 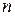 векторов в пространстве
векторов в пространстве  ).
).
Системы векторов 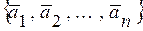 – линейно зависима (линейно независима) в
– линейно зависима (линейно независима) в  тогда и только тогда, когда определитель, составленный из координат этих векторов, равен нулю (отличен от нуля).
тогда и только тогда, когда определитель, составленный из координат этих векторов, равен нулю (отличен от нуля).
Пример 2. Определить, являются ли линейно зависимыми вектора
 ,
,  и
и  ?
?
Решение. Составим и вычислим определитель из координат векторов:

Т.к. 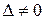 , то векторы
, то векторы 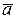 ,
, 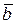 и
и 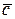 - линейно независимы. n
- линейно независимы. n
Теорема 4. Любые  векторов линейно зависимы в пространстве
векторов линейно зависимы в пространстве  .
.
Замечание. Остается рассмотреть ситуацию, когда количество векторов в системе больше двух, но меньше 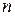 (например, три вектора в пространстве
(например, три вектора в пространстве  ). Итак, выясним линейную зависимость (независимость) системы
). Итак, выясним линейную зависимость (независимость) системы  в пространстве
в пространстве  , где
, где  . Рассмотрим матрицу
. Рассмотрим матрицу  , составленную из координат этих векторов, и вычислим ее ранг. С учетом теоремы 5, делаем вывод: если
, составленную из координат этих векторов, и вычислим ее ранг. С учетом теоремы 5, делаем вывод: если 
 , то система линейно независима, а если
, то система линейно независима, а если 
 , то система
, то система 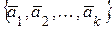 - линейно зависима.
- линейно зависима.
Дата публикования: 2014-11-04; Прочитано: 712 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
