 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Комплексные числа
|
|
Комплексные числа применяются, в частности, для решения квадратных уравнений. Так, оставаясь в области множества действительных чисел, невозможно решить квадратное уравнение, дискриминант которого меньше нуля.
Комплексным числом называется выражение вида  , где
, где 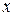 и
и  - действительные числа,
- действительные числа,  - мнимая единица.
- мнимая единица.
Число 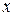 называется действительной частью числа
называется действительной частью числа  и обозначается
и обозначается  , а число
, а число  - мнимой частью числа
- мнимой частью числа  и обозначается
и обозначается  , т.е.
, т.е.  ,
,  .
.
Действительное число 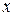 является частным случаем комплексного
является частным случаем комплексного  при
при  . Комплексные числа вида
. Комплексные числа вида  , не являющиеся действительными (т.е. при
, не являющиеся действительными (т.е. при  ), называются мнимыми, а при
), называются мнимыми, а при  ,
,  , т.е. числа вида
, т.е. числа вида  - чистомнимыми.
- чистомнимыми.
Числа  и
и 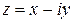 называются сопряженными. Два комплексных числа
называются сопряженными. Два комплексных числа  и
и  называются равными, если равны их действительные и мнимые части, т.е.
называются равными, если равны их действительные и мнимые части, т.е. 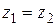 , если
, если  ,
,  . В частности
. В частности  , если
, если  и
и  .
.
Арифметические операции на множестве комплексных чисел определяются следующим образом:
1. Сложение (вычитание) комплексных чисел:
 .
.
2. Умножение комплексных чисел:
 .
.
В частности, 
3. Деление двух комплексных чисел:

Пример 7. Даны два комплексных числа  и
и  . Найти
. Найти  ,
,  ,
,  ,
,  .
.
Решение.
 ,
,
 ,
,
 ,
,
 .
.
Умножая числитель и знаменатель на сопряженное делителю комплексное число  , получаем:
, получаем:
 .n
.n
Пример 8. Решить квадратное уравнение  .
.
Решение.
Используя, хорошо известную формулу нахождения корней квадратного уравнения, получим:
 .
.
Проверить правильность решения можно с помощью теоремы Виета:

Действительно,
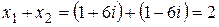
 .n
.n
Если для геометрического изображения действительных чисел используются точки числовой прямой, то для представления комплексных чисел служат точки координатной плоскости  .
.
Плоскость называется комплексной, если каждому комплексному числу  ставится в соответствие точка плоскости
ставится в соответствие точка плоскости  , причем это соответствие взаимно однозначное. Оси
, причем это соответствие взаимно однозначное. Оси 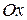 и
и 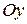 , на которых расположены действительные числа
, на которых расположены действительные числа  и чисто мнимые числа
и чисто мнимые числа  , называются соответственно действительной и мнимой осями (рис. 4).
, называются соответственно действительной и мнимой осями (рис. 4).

С каждой точкой  комплексной плоскости связан радиус-вектор этой точки
комплексной плоскости связан радиус-вектор этой точки  , длина которого
, длина которого  называется модулем комплексного числа
называется модулем комплексного числа  и обозначается
и обозначается  :
:
 .
.
Угол  , образованный радиус-вектором
, образованный радиус-вектором  с осью
с осью 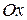 , называется аргументом комплексного числа
, называется аргументом комплексного числа  и обозначается
и обозначается  .
.
Очевидно, что
 ,
,  .
.
Следовательно, комплексное число  можно представить как:
можно представить как:
 .
.
Данное представление комплексного числа, где  ,
,  , называется тригонометрической формой комплексного числа.
, называется тригонометрической формой комплексного числа.
Дата публикования: 2014-11-04; Прочитано: 404 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
