 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Аналитическая геометрия
|
|
199) В уравнении прямой y= kx+b коэффициент k равен
а) тангенсу угла наклона прямой к положительному направлению оси абсцисс;
б) тангенсу угла наклона прямой к отрицательному направлению оси абсцисс;
в) тангенсу угла наклона прямой к отрицательному направлению оси ординат;
г) тангенсу угла наклона прямой к положительному направлению оси ординат;
200) Расстояние d между двумя точками М1(x1) и М2(x2) координатной оси находится по формуле:
а) d=  ;
;
б) d=  ;
;
в) d=  ;
;
г) d=  ;
;
201) Любая прямая на плоскости может быть задана уравнением первого порядка Ах + Ву + С = 0, причем постоянные А, В не равны нулю одновременно, т.е. А2 + В2 ≠ 0. Это уравнение первого порядка называют
а) общим уравнением прямой;
б) уравнением прямой проходящей через две точки;
в) уравнение прямой по точке и угловому коэффициенту;
г) уравнение прямой по точке и направляющему вектору.
202) Как называется уравнение прямой линии, пересекающей ось Ox в точке (a,0) и ось Oy в точке (0,b):

а) уравнением прямой проходящей через две точки;
б) уравнение прямой по точке и угловому коэффициенту;
в) общим уравнением прямой;
г) уравнение прямой в отрезках.
203) Расстояние от точки М  до прямой Ах + Ву + С =0 вычисляется по формуле:
до прямой Ах + Ву + С =0 вычисляется по формуле:
а) d= 
б) d= 
в) d= 
г) d= 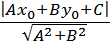
204) Даны вершины треугольника А(0; 1), B (6; 5), C (12; -1). Найти уравнение высоты, проведенной из вершины С.
а) 4 x + 5 y – 34 = 0;
б) 3x + 2 y –39 = 0;
в) 3 x + 2 y – 34 = 0;
г) 3 x + 2 y +39 = 0.
205) Найдите правильное определение по данной формуле

а) Если заданы две прямые y =  x+
x+ 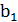 , y =
, y =  , то тупой угол между этими прямыми будет определяться как;
, то тупой угол между этими прямыми будет определяться как;
б) Если заданы две прямые y =  , y =
, y =  , то острый угол между этими прямыми будет определяться как;
, то острый угол между этими прямыми будет определяться как;
в) Если заданы две прямые y =  , y =
, y =  , то острый угол между этими прямыми будет определяться как;
, то острый угол между этими прямыми будет определяться как;
г) Если заданы две прямые y =  , y =
, y =  , то тупой угол между этими прямыми будет определяться как;
, то тупой угол между этими прямыми будет определяться как;
206) Найти уравнение прямой, проходящей через точки А(1, 2) и В(3, 4).
а) x-y+3=0;
б) x-y+1=0;
в) x-y+17=0;
г) x-2y+8=0.
207) Составить уравнение прямой, проходящей через точку А(-2, -3) и начало координат.
а) 3x-2y=0;
б) x+2y=0;
в) 5x+5y=0;
г) 4x-7y=0.
208) Определить угол между прямыми: y = -x + 7; y = x + 1.
а) 45⁰;
б) 30⁰;
в) 0⁰;
г) 900.
209) Уравнение с переменными x и y, которому удовлетворяют координаты любой точки этой линии и только они, называется
а) уравнением прямой проходящей через две точки;
б) уравнением линии;
в) уравнением прямой по точке и угловому коэффициенту;
г) уравнением прямой по точке и направляющему вектору.
210) Прямая 2x + y - 6 = 0 пересекает ось Ox в точке
а) (7, 0);
б) (9, 0);
в) (2, 0);
г) (3, 0).
211) Прямая задана общим уравнением 2х-3у+6=0. Составить для этой прямой уравнение «в отрезках»
а) 
б) 
в) 
г) x+y=1.
212) Как называется угол α, на который нужно повернуть ось Ох, чтобы её положительное направление совпало с одним из направлений прямой.
а) Углом наклона данной прямой к оси Ох;
б) углом наклона данной прямой к оси Оу;
в) углом наклона данной прямой к началу координат;
г) углом кривой.
213) Прямая задана общим уравнением 4х+2у-2=0. Составить для этой прямой уравнение с угловым коэффициентом.
а) у=х+1;
б) у=-2х+1;
в) у=-6х+7;
г) у=3х+1.
214) Две прямые заданы уравнениями у=2х+3 и у=-3х+2. найти угол между этими прямыми.
а) 30⁰;
б) 60⁰;
в) 45⁰;
г) 90⁰.
215) Условием чего является равенство угловых коэффициентов?
а) параллельности двух прямых;
б) пересечения двух прямых;
в) перпендикулярности двух прямых;
г) совпадения двух прямых.
216) Составить уравнение плоскости, проходящей через ось  и через точку A (1; -1;3);
и через точку A (1; -1;3);
а) у+3z=0;
б) 3y+z=0;
в) 3x-z=0;
г) x+y=0;
217) Составить уравнение плоскости, проходящей через точку M (4; -4; 2) и параллельной плоскости XOZ.
А) x-4=0;
Б) z-2=0
В) y+4=0
Г) x-2z=0
218) Из точки M (-1; -1; 4) опущен на плоскость перпендикуляр; его основание
N (2; 1; 3). Составить уравнение плоскости.
А) 3x+2y-z-5=0;
Б) 3x+2y-z+9=0;
В) 3x+y+z=0;
Г) x-y+z-4=0;
219) Плоскость проходит через ось 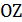 и составляет с плоскостью
и составляет с плоскостью
 угол
угол  . Составить её уравнение.
. Составить её уравнение.
А) 4x+y=0;
Б) 3x-y=0;
В)x+3y=0;
Г) x+3y=0 и 3x-y=0;
220) Составить уравнение плоскости, проходящей через точку  (2; -3; 1) параллельно векторам
(2; -3; 1) параллельно векторам  = (-3; 2; -1) и
= (-3; 2; -1) и 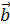 = (1; 2; 3).
= (1; 2; 3).
А) 4x+y-2z=0
Б) x-y+9=0
В) x+y-z+2=0
Г) y-z=0
221) Составить уравнение плоскости, проходящей через точки  (3; -1; 2),
(3; -1; 2),
 (4; 1; -1) и
(4; 1; -1) и  (2; 0; 2).
(2; 0; 2).
А) 3x+3y+z-8=0;
Б) x-y+z=0;
В) 4x+12y=0;
Г) 4y+z-3=0;
222) Составить уравнение прямой, проходящей через точку  (1; -3; 5) параллельно прямой
(1; -3; 5) параллельно прямой 
А)  =
=  =
= 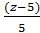 ;
;
Б)  =
=  ;
;
В)  =
=  ;
;
Г)  =
=  =
=  ;
;
223) Составить уравнение прямой, проходящей через точку  (3; -2; 4) перпендикулярно плоскости
(3; -2; 4) перпендикулярно плоскости  .
.
А)  =
=  =
=  ;
;
Б)  =
=  ;
;
В)  =
=  =
=  ;
;
Г)  =
=  ;
;
224) Найти проекцию точки A (4; -3; 1) на плоскость  .
.
А) (3; -4; 0);
Б) (0; 9; -2);
В) (-1; 12; 8);
Г) (5; -1; 0);
225) Найти проекцию точки A (1; 2; 1) на прямую  .
.
А) (0; 9; -2);
Б) ( ;
;  ;
;  );
);
В) ( ;
;  ;
;  );
);
Г) (0; 3; -2);
226) Расстояние d от точки A (x0, у0, z0) до плоскости Ах+Ву+Cz+D=0, находится по формуле:
А) d = 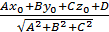 ;
;
Б) d =  ;
;
В) d=  ;
;
Г) d=  ;
;
227) Условие параллельности двух плоскостей:
А)  ;
;
Б)  ;
;
В)  =
=  =
=  ;
;
Г) 
228) Условие перпендикулярности двух плоскостей:
А)  ;
;
Б)  =
=  =
=  ;
;
В) 
Г)  +
+  +
+  =0
=0
229) Условие параллельности двух прямых в пространстве:
А)  =
=  ;
;
Б) A=B=C=D;
В)  =
=  =
=  ;
;
Г)  =
=  =
= 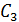 ;
;
230) Условия перпендикулярности двух прямых в пространстве:
А)  +
+  +
+ 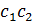 =0;
=0;
Б)  +
+  +
+  =0;
=0;
В) 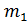 =
=  ;
;
Г) a+b+c=0;
231) Условие параллельности прямой и плоскости:
А) 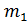 =
=  ;
;
Б)Am=Bn=Cp;
В)am+bn+cp=0;
Г) Am+Bn+Cp=0;
232) Условие перпендикулярности прямой и плоскости:
А) Am=Bn=Cp;
Б) 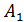 =
=  =
= 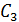 ;
;
В)  =
=  =
=  ;
;
Г) am+bn+cp=0;
Кривые второго порядка (окружность, эллипс, гипербола, парабола)
233) Как выглядит общее уравнение кривой 2-го порядка?
а) А  +С
+С  +Dx+Еу+F=0;
+Dx+Еу+F=0;
б) А  +Вху+С
+Вху+С  + F=0;
+ F=0;
в) А  +Вху+С
+Вху+С  +Dx+Еу+F=0;
+Dx+Еу+F=0;
г) Dx+Еу+F=0;
234) Уравнение окружности выглядит (общий вид)
а)  +
+  =
= 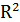 ;
;
б)  +
+  =
= 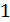 ;
;
в)  +
+  =
=  ;
;
г)  +
+  =
= 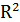 ;
;
235) Что такое эллипс?
а) множество точек, равноудаленных от центра;
б) множество точек, сумма расстояний от которых до 2-х данных точек (фокусов) постоянно;
в) множество точек, модуль разности расстояний от которых до 2-х данных точек (фокусов) постоянно;
г) множество точек, равноудаленных от данной точки (фокуса) и данной прямой (директрисы).
236) Что характеризует форму эллипса?
а) градиент;
б) экспонента;
в) эксцентриситет;
г) фокальное расстояние.
237) Окружность- это..
а) множество точек, равноудаленных от центра;
б) множество точек, сумма расстояний от которых до 2-х данных точек (фокусов) постоянно;
в) множество точек, модуль разности расстояний от которых до 2-х данных точек (фокусов) постоянно;
г) множество точек, равноудаленных от данной точки (фокуса) и данной прямой (директрисы).
238) Какие рамки имеет эксцентриситет?
а) (0;1);
б) [0;1];
в) [0;1);
г) (-1;1).
239) Гипербола-это
а) множество точек, равноудаленных от центра;
б) множество точек, сумма расстояний от которых до 2-х данных точек (фокусов) постоянно;
в) множество точек, модуль разности расстояний от которых до 2-х данных точек (фокусов) постоянно;
г) множество точек, равноудаленных от данной точки (фокуса) и данной прямой (директрисы).
240) Парабола - это
а) множество точек, равноудаленных от центра;
б) множество точек, сумма расстояний от которых до 2-х данных точек (фокусов) постоянно;
в) множество точек, модуль разности расстояний от которых до 2-х данных точек (фокусов) постоянно;
г) множество точек, равноудаленных от данной точки (фокуса) и данной прямой (директрисы).
241) Составить уравнение окружности, проходящей через точку (5;3) с центром в точке пересечения прямых 5х-3у-13=0 и х+4у+2=0
а)  +
+  =0;
=0;
б)  +
+  =25;
=25;
в) (у-2)+(х+4)=64;
г)  +
+  =144.
=144.
242) Определить эксцентриситет эллипса 3  +4
+4  -12=0
-12=0
а)0,6;
б)0,5;
в)0,3;
г)1.
243) Найти радиус окружности 3  +3
+3  -6х+8у=0
-6х+8у=0
а) 5/3;
б) 6/5;
в) 5/8;
г) 3/7.
244) Составить уравнение окружности, касающейся оси Оу в начале координат и пересекающей ось Ох в точке М(6;0)
а)  +
+  =33;
=33;
б)  +
+  =9;
=9;
в)  +
+  =4;
=4;
г)  +
+  =9.
=9.
245) Составить уравнение окружности, если она проходит через точки А(3;1), В(-1;3), а центр лежит на прямой 3х-у-2=0
а)  +
+  =36;
=36;
б)  +
+  =9;
=9;
в)  +
+  =10.
=10.
246) Составить уравнение окружности, проходящей через точки пересечения окружности  +
+  +4х-4у=0 с прямой х+у=0 и точку М(4;4)
+4х-4у=0 с прямой х+у=0 и точку М(4;4)
а)  +
+  =16;
=16;
б)  +
+  =25;
=25;
в)  +
+  =64.
=64.
Дата публикования: 2014-11-04; Прочитано: 1087 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
