Квадратичные формы

179) Вставьте пропущенное слово:

Квадратичной формой L (x₁,x_x,..,x_n) от n переменных называется ………, каждый член которой является либо квадратом одной из переменных, либо произведением двух разных переменных, взятых с некоторым коэффициентом.

а) разность;

б) сумма;

в) произведение;

г) отношение.

180) В матричной записи квадратичная форма имеет вид:

а) L=XA;

б) L=AXX^’;

в) L=XAX^’;

г) L=A^’X.

181) Если квадратичная форма знакоопределенная, то все главные (угловые) миноры ее матрицы ………:

а) равны нулю;

б) отличны от нуля;

в) всегда отрицательны;

г) всегда положительны.

182) Какая функция не является квадратичной формой?

а) x₁²+3x₁x₂+x₂²;

б) -x₁x₂;

в) x₁²-x₁x₂+x₃²;

г) x₁²+3x₁+1.

183) Квадратичная форма отрицательно определена тогда и только тогда, когда (Критерий Сильвестра):

а) M₁<0, M₂>0, M₃<0 … и т.д.;

б) М₁>0, M₂>0, M₃>0…и т.д.;

в) M₁<0, M₂<0, M₃<0 и т.д.;

г) нет верных вариантов.

184) Пусть A – матрица квадратичной формы. При невырожденном линейном преобразовании X=CY (где Х=(х₁, х, …, x_n)’, Y=(y₁, y₂, …, y_n)’, С- матрица линейного преобразования) матрица квадратичной формы имеет вид:

а) А^*=САС’

б) А^*=САС

в) А^*=С’CA

г) А^*=C’AC

185) Квадратичная форма положительно определена тогда и только тогда, когда (Критерий Сильвестра):

а) все главные (угловые) миноры матрицы А положительны;

б) все главные (угловые) миноры матрицы А отрицательны;

в) все главные миноры матрицы А нечетного порядка отрицательны, а матрицы четного порядка положительны;

г) все собственные значения матрицы А отрицательны.

186) Найти квадратичную форму соответствующую матрице

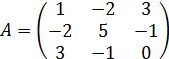
а) x₁²+5x₂²-8x₁x₂+6x₁x₃-2x₂x₃;

б) x₁²+5x₂²-4x₁x₂+6x₁x₃-2x₂x₃;

в) x₁²+5x₂²-4x₁x₂+6x₁x₃-x₂x₃;

г) x₁²-5x₂²-4x₁x₂+6x₁x₃-2x₂x₃.

187) Привести к каноническому виду квадратичную форму L=x₁²+2x₂²+7x₃²+2x₁x₂+2x₁x₃+4x₂x₃ .

а) y₁²-y₂²+5y₃²;

б) -y₁²+y₂²+y₃²;

в) y₁²+y₂²+5y₃²;

г) y₁²+y₂²-5y₃².

188) Исследовать на знакоопределенность квадратичную форму L=2x₁²+x₂²+4x₃²+2x₁x₂-4x₁x₃-2x₂x₃ .

а) положительно определенная;

б) отрицательно определенная;

в) не является знакоопределнной;

г) все варианты не верны.

189) Написать квадратичную форму L=3x₁²+x₂²-x₁x₂ в матричном виде.

а) А= ;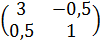

б) А= ;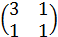

в) А= ;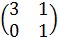

г) А= ;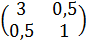

190) Квадратичная форма отрицательно определена тогда и только тогда, когда все ее собственные значения:

а) положительны;

б) четные - положительны, нечетные отрицательны;

в) отрицательны;

г) все варианты неверны.

191) Квадратичная форма положительно определена тогда и только тогда, когда ее собственные значения:

а) положительны;

б) четные - положительны, нечетные отрицательны;

в) отрицательны;

г) все варианты неверны.

192) Дана квадратичная форма L=(x₁,x₂)=3x₁²-x₂²+4x₁x₂. Найти квадратичную форму L=(y₁,y₂), полученную из данной линейным преобразованием x₁=2y₁-y₂ и x₂=y₁+y₂.

а) 19y₁²- 10y₁y₂ - 2y₂²;

б) 19y₁²- 10y₁y₂ -y₂²;

в) y₁²- 10y₁y₂ - 2y₂²;

г) 19y₁²- y₁y₂ - 2y₂².

193) Написать квадратичную форму L=2x₁²+3x₂² -2x₃²+x₁x₂+2x₁x₃+3x₂x₃ в матричном виде.

а) А= ;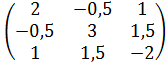

б) А= ;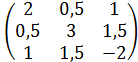

в) А= ;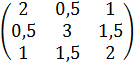

г) А= .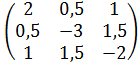

194) Привести к каноническому виду квадратичную форму

L=2x₁² -3x₃²-4x₁x₂+4x₁x₃-8x₂x₃

а) y₁²-y₂²;

б) y₁²-3y₃²;

в) y₂²-7y₃²;

г) 3y₁²+y₂².

195) Исследовать на знакоопределенность квадратичную форму L=x₁²+4x₂²+3x₃²-2x₁x₂.

а) не является знакоопределнной;

б) отрицательно определенная;

в) положительно определенная;

г)все варианты не верны

196)Дана квадратичная форма L=(x₁,x₂)=2x₁²+3x₂²-x₃²+x₁x₂. Найти квадратичную форму L=(y₁,y₂,y₃), полученную из данной линейным преобразованием x₁=-y₁+2y₂, x₂=3y₁+y₂+y₃ , x₃=-2y₁-y₂.

а)y₁²+y₂² +y₃²+ 11y₁y₂ +17 y₁y₃ + 8y₂y₃;

б) 22y₁²+12y₂² +3y₃²+ y₁y₂ + y₁y₃ +y₂y₃;

в) 22y₁²+12y₂² +y₃²+ y₁y₂ +17 y₁y₃ + 8y₂y₃;

г) 22y₁²+12y₂² +3y₃²+ 11y₁y₂ +17 y₁y₃ + 8y₂y₃.

197) Написать квадратичную форму L=2x₁²+x₂²+4x₁x₂ в матричном виде.

а) А= ;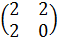

б) А= ;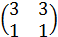

в) А= ;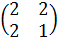

г) А= .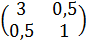

198) Найти ранг квадратичной формы L=x₁²+x₂²+х₃² +2x₁x₂.

а) Rank=2;

б) Rank=4;

в) Rank=1;

г) Rank=3.