 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Г) Методом главных компонент
|
|
23) Если матрица имеет обратную, то:
а)  0 и
0 и 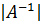 =
=  ;
;
б) 
 1 и
1 и 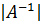 =
=  ;
;
в)  ≥ 1 и
≥ 1 и 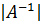 =
=  ;
;
г)  0 и
0 и 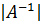 ≠
≠  .
.
24)Если определитель матрицы равен нулю, то:
а) Обратная матрица к ней существует;
б) Обратная матрица к ней не существует;
в) Обратная матрица равна единичной;
г) Обратная матрица нулевая.
25) Если обратная матрица существует, то:
а) Она единственна;
б) Их множество;
в) Их две;
г) Ее определитель равен нулю.
26) Обратная матрица для квадратной матрицы  существует тогда и только тогда,
существует тогда и только тогда,
а) Когда ее определитель не равен нулю;
б) Когда ее определитель равен нулю;
в) Когда матрица  - вырожденная;
- вырожденная;
г) Когда ее ранг больше нуля.
27) Найдите обратную матрицу для матрицы А=  .
.
а)  =
= 
 ;
;
б)  =
= 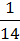
 ;
;
в) обратной матрицы не существует;
г)  =
= 
 .
.
28) Квадратная матрица  называется вырожденной, если
называется вырожденной, если
а)  = 0;
= 0;
б)  0;
0;
в)  = 1;
= 1;
г) А = Е.
29) Понятие обратной матрицы вводится:
а) Только для квадратных матриц;
б) Для всех матриц;
в) Только для единичных матриц;
г) только для диагональных матриц.
30)Чтобы найти обратную матрицу нужно:
а) Найти алгебраические дополнения Aij всех элементов матрицы A и составить матрицу A', элементами которой являются числа Aij , а затем разделить их на определитель матрицы A и транспонировать полученную матрицу;
б) Найти алгебраические дополнения Aij всех элементов матрицы A и составить матрицу A', элементами которой являются числа Aij , а затем разделить их на определитель матрицы A;
в) Найти алгебраические дополнения Aij всех элементов матрицы A и составить матрицу A', элементами которой являются числа Aij , а затем транспонировать полученную матрицу;
г) Найти алгебраические дополнения Aij всех элементов матрицы A и составить матрицу A', элементами которой являются числа Aij .
31)Найти обратную матрицу для матрицы  .
.
а) обратной матрицы не существует;
б)  ;
;
в)  .
.
г) единичная матрица.
32) A =  , B =
, B =  .
.
Требуется найти матрицу  (AB).
(AB).
а)  ;
;
б)  ;
;
в)  ;
;
г)  .
.
33) Найти обратную матрицу для матрицы: A = 
а)  =
=  ;
;
б)  =
=  ;
;
в)  =
= 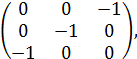
г)  =
= 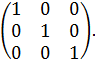
34) Найти обратную матрицу для матрицы: A = 
а)  =
=  ;
;
б)  =
=  ;
;
в)  =
= 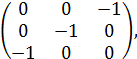
г)  =
= 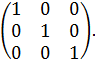
35) Определитель обратной матрицы
а) равен определителю самой матрицы;
б) при умножении на определитель самой матрицы дает 1; в) при умножении на определитель самой матрицы дает -1;г) в сумме с определителем самой матрицы дает 0.36) Выберите верное равенство:
а)  ;
;
б)  ;
;
в)  ;
;
г) 
37) Выберите верное равенство:
а)  ;
;
б)  ;
;
в)  ;
;
г)  .
.
38) Найти обратную матрицу для A =  .
.
а)  ;
;
б)  ;
;
в)  .
.
г) обратной матрицы не существует.
39) Если необходимо решить систему линейных уравнений  , (b — ненулевой вектор) где
, (b — ненулевой вектор) где  — искомый вектор, и если
— искомый вектор, и если  существует, то
существует, то
а)  ;
;
б)  ;
;
в)  ;
;
г)  .
.
40) Ранг матрицы — это
а) наибольший из порядков ее миноров, не равных нулю;
б) результат произведения диагональных элементов матрицы;
в) наименьший из порядков ее миноров, не равных нулю;
г) результат сложения диагональных элементов матрицы.
41)Если все миноры матрицы равны нулю, то
а) Ранг матрицы >0;
б) Ранг матрицы<0;
в) Ранг матрицы = 0;
г) Ранг матрицы ≠0.
42)Ранг матрицы, полученной транспонированием
а) равен единице;
б) равен рангу исходной матрицы;
в) равен нулю;
г) ≥1.
43) При элементарных преобразованиях ранг матрицы
а) меняется;
б) становится равным нулю;
в) становится равным единице;
г) не меняется.
44) Ранг матрицы А обозначают символом
а) Rang A;
б) det A;
в) AT;
г) ∑A.
45) Ранг матрицы можно вычислить
а) Методом алгебраических дополнений;
б) Методом Гаусса;
в) Методом Крамера;
г) всеми вышеперечисленными.
Дата публикования: 2014-11-04; Прочитано: 320 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
