Логарифмическое дифференцирование

Дифференцирование многих функций упрощается, если их предварительно прологарифмировать. Для этого поступают следующим образом. Если требуется найти y ' из уравнения y=f(x), то можно:

1. Прологарифмировать обе части уравнения (по основанию е) ln y = ln f(x) = j(x).

2. Продифференцировать обе части равенства, считая ln y сложной функцией от переменной x: .

3. Выразить y ' = y ·j'(x) = f(x) ·(ln x)'.

Примеры.

1. y = x ^a – степенная функция с произвольным показателем.

.

2.

ПОКАЗАТЕЛЬНО-СТЕПЕННАЯ ФУНКЦИЯ И ЕЕ ДИФФЕРЕНЦИРОВАНИЕ

Показательно-степенной функцией называется функция вида y = u^v, где u=u(x), v=v(x).

Логарифмическое дифференцирование применяется для нахождения производной от показательно-степенной функции.

Примеры.

1.

2. .

ТАБЛИЦА ПРОИЗВОДНЫХ

Объединим в одну таблицу все основные формулы и правили дифференцирования, выведенные ранее. Всюду будем полагать u=u(x), v=v(x), С=const. Для производных основных элементарных функций будем пользоваться теоремой о производной сложной функции.

1. .

2. .

3. .

4. .

5. .

а) .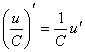

б) .

6. .

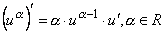7. .

.

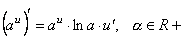8.

9. .

10. .

11. .

12. .

13. .

14. .

15. .

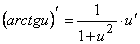16. .

17. .

Примеры.

1.

2.

3. . Найти y' (–1).