Теорема о производной обратной функции

Докажем теорему, позволяющую находить производную функции y=f(x), зная производную обратной функции.

Теорема. Если для функции y=f(x) существует обратная функция x=g(y), которая в некоторой точке у ₀ имеет производную g '(v₀), отличную от нуля, то в соответствующей точке x₀ = g (x₀) функция y=f(x) имеет производную f '(x₀), равную , т.е. справедлива формула .

Доказательство. Т.к. x=g(y) дифференцируема в точке y₀, то x=g(y) непрерывна в этой точке, поэтому функция y=f(x) непрерывна в точке x₀ = g (y₀). Следовательно, при Δ x →0 Δ y →0.

Покажем, что .

Пусть . Тогда по свойству предела . Перейдем в этом равенстве к пределу при Δ y →0. Тогда Δ x →0 и α(Δx)→0, т.е. .

Следовательно,

,

что и требовалось доказать.

Эту формулу можно записать в виде .

Рассмотрим применение этой теоремы на примерах.

Примеры.

1. y = e^x. Обратной для этой функции является функция x = ln y. Мы уже доказали, что . Поэтому согласно сформулированной выше теореме

Итак,

(ex) ' = ex

2. Аналогично можно показать, что (a ^x) ' = a ^x·ln a. Докажите самостоятельно.

3. y = arcsin x. Рассмотрим обратную функцию x = sin y. Эта функция в интервале – π/2< y <π/2 монотонна. Ее производная x ' = cos y не обращается в этом интервале в нуль. Следовательно, по теореме о производной обратной функции

.

Но на (–π/2; π/2) .

Поэтому

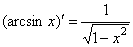
4. Аналогично

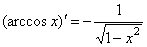
Докажите самостоятельно.

5. y = arctg x. Эта функция по определению удовлетворяет условию существования обратной функции на интервале –π/2< y < π/2. При этом обратная функция x = tg y монотонна. По ранее доказанному .

Следовательно, y ' = cos² y. Но .

Поэтому

6.

7. Используя эти формулы, найти производные следующих функций