 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Определение производной
|
|
Пусть имеем некоторую функцию y=f(x), определенную на некотором промежутке. Для каждого значения аргумента x из этого промежутка функция y=f(x) имеет определенное значение.
Рассмотрим два значения аргумента: исходное x 0 и новое x. 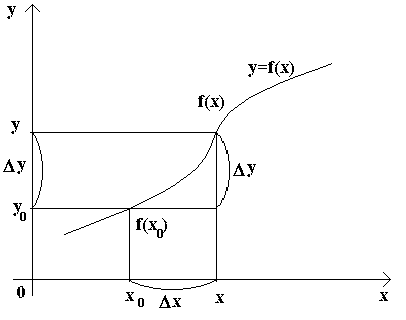 Разность x– x 0 называется приращением аргумента x в точке x 0 и обозначается Δx. Таким образом, Δx = x – x 0 (приращение аргумента может быть как положительным, так и отрицательным). Из этого равенства следует, что x=x 0 +Δx, т.е. первоначальное значение переменной получило некоторое приращение. Тогда, если в точке x 0 значение функции было f(x 0 ), то в новой точке x функция будет принимать значение f(x) = f(x 0 +Δx).
Разность x– x 0 называется приращением аргумента x в точке x 0 и обозначается Δx. Таким образом, Δx = x – x 0 (приращение аргумента может быть как положительным, так и отрицательным). Из этого равенства следует, что x=x 0 +Δx, т.е. первоначальное значение переменной получило некоторое приращение. Тогда, если в точке x 0 значение функции было f(x 0 ), то в новой точке x функция будет принимать значение f(x) = f(x 0 +Δx).
Разность y – y 0 = f(x) – f(x 0 ) называется приращением функции y = f(x) в точке x 0 и обозначается символом Δy. Таким образом,
| Δy = f(x) – f(x 0 ) = f(x 0 +Δx) - f(x 0 ). | (1) |
Обычно исходное значение аргумента x 0 считается фиксированным, а новое значение x – переменным. Тогда y 0 = f(x 0 ) оказывается постоянной, а y = f(x) – переменной. Приращения Δy и Δx также будут переменными и формула (1) показывает, что Δy является функцией переменной Δx.
Составим отношение приращения функции к приращению аргумента
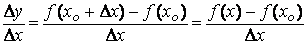
Найдем предел этого отношения при Δx →0. Если этот предел существует, то его называют производной данной функции f(x) в точке x 0 и обозначают f '(x 0). Итак,
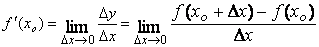 .
.
Производной данной функции y = f(x) в точке x 0 называется предел отношения приращения функции Δ y к приращению аргумента Δ x, когда последнее произвольным образом стремится к нулю.
Заметим, что для одной и той же функции производная в различных точках x может принимать различные значения, т.е. производную можно рассматривать как функцию аргумента x. Эта функция обозначается f '(x)
Производная обозначается символами f ' (x),y ', 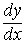 . Конкретное значение производной при x = a обозначается f '(a) или y ' |x=a.
. Конкретное значение производной при x = a обозначается f '(a) или y ' |x=a.
Операция нахождения производной от функции f(x) называется дифференцированием этой функции.
Для непосредственного нахождения производной по определению можно применить следующее практическое правило:
1. Придать x приращение Δ x и найти наращенное значение функции f(x + Δx).
2. Найти приращение функции Δy = f(x + Δx) – f(x).
3. Составить отношение 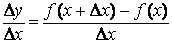 и найти предел этого отношения при Δ x ∞0.
и найти предел этого отношения при Δ x ∞0.
Примеры.
1. Найти производную функции y = x2
а) в произвольной точке;
б) в точке x = 2.
а)
1. f(x + Δx) = (x + Δx) 2;
2. Δy = (x + Δx)2 – x2=2xΔx– x 2;
3. 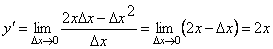 .
.
б) f '(2) = 4
2. Используя определение найти производную функции 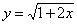 в произвольной точке.
в произвольной точке.
1. 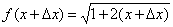 .
.
2. 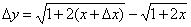
3. 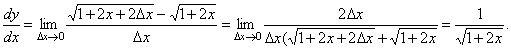
Дата публикования: 2015-11-01; Прочитано: 456 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
