 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Понятие обратной функции
|
|
Начнем с примера. Рассмотрим функцию y= x3. Будем рассматривать равенство y = x3 как уравнение относительно x. Это уравнение для каждого значения у определяет единственное значение x: 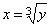 . Геометрически это значит, что всякая прямая параллельная оси Ox пересекает график функции y= x3 только в одной точке. Поэтому мы можем рассматривать x как функцию от y. Функция . Геометрически это значит, что всякая прямая параллельная оси Ox пересекает график функции y= x3 только в одной точке. Поэтому мы можем рассматривать x как функцию от y. Функция 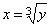 называется обратной по отношению к функции y= x3.
Прежде чем перейти к общему случаю, введем определения.
Функция y = f(x) называется возрастающей на некотором отрезке, если большему значению аргумента x из этого отрезка соответствует большее значение функции, т.е. если x 2> x 1, то f(x 2 ) > f(x 1 ).
Аналогично функция называется убывающей, если меньшему значению аргумента соответствует большее значение функции, т.е. если х 2 < х 1, то f(x 2 ) > f(х 1 ).
Итак, пусть дана возрастающая или убывающая функция y= f(x), определенная на некотором отрезке [ a; b ]. Для определенности будем рассматривать возрастающую функцию (для убывающей все аналогично).
Рассмотрим два различных значения х 1 и х 2. Пусть y 1 =f(x 1 ), y 2 =f(x 2 ). Из определения возрастающей функции следует, что если x 1< x 2, то у 1< у 2. Следовательно, двум различным значениям х 1 и х 2 соответствуют два различных значения функции у 1 и у 2. Справедливо и обратное, т.е. если у 1< у 2, то из определения возрастающей функции следует, что x 1< x 2. Т.е. вновь двум различным значениям у 1 и у 2 соответствуют два различных значения x 1 и x 2. Т.о., между значениями x и соответствующими им значениями y устанавливается взаимно однозначное соответствие, т.е. уравнение y=f(x) для каждого y (взятого из области значений функции y=f(x)) определяет единственное значение x, и можно сказать, что x есть некоторая функция аргумента y: x= g(у). называется обратной по отношению к функции y= x3.
Прежде чем перейти к общему случаю, введем определения.
Функция y = f(x) называется возрастающей на некотором отрезке, если большему значению аргумента x из этого отрезка соответствует большее значение функции, т.е. если x 2> x 1, то f(x 2 ) > f(x 1 ).
Аналогично функция называется убывающей, если меньшему значению аргумента соответствует большее значение функции, т.е. если х 2 < х 1, то f(x 2 ) > f(х 1 ).
Итак, пусть дана возрастающая или убывающая функция y= f(x), определенная на некотором отрезке [ a; b ]. Для определенности будем рассматривать возрастающую функцию (для убывающей все аналогично).
Рассмотрим два различных значения х 1 и х 2. Пусть y 1 =f(x 1 ), y 2 =f(x 2 ). Из определения возрастающей функции следует, что если x 1< x 2, то у 1< у 2. Следовательно, двум различным значениям х 1 и х 2 соответствуют два различных значения функции у 1 и у 2. Справедливо и обратное, т.е. если у 1< у 2, то из определения возрастающей функции следует, что x 1< x 2. Т.е. вновь двум различным значениям у 1 и у 2 соответствуют два различных значения x 1 и x 2. Т.о., между значениями x и соответствующими им значениями y устанавливается взаимно однозначное соответствие, т.е. уравнение y=f(x) для каждого y (взятого из области значений функции y=f(x)) определяет единственное значение x, и можно сказать, что x есть некоторая функция аргумента y: x= g(у).
| 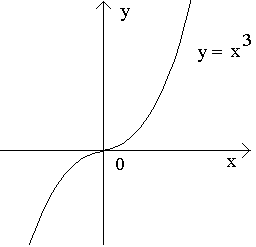 
|
Эта функция называется обратной для функции y=f(x). Очевидно, что и функция y=f(x) является обратной для функции x=g(у).
Заметим, что обратная функция x=g(y) находится путем решения уравнения y=f(x) относительно х.
Пример. Пусть дана функция y = ex. Эта функция возрастает при –∞ < x <+∞. Она имеет обратную функцию x = ln y. Область определения обратной функции 0 < y < + ∞.
Сделаем несколько замечаний.
Замечание 1. Если возрастающая (или убывающая) функция y=f(x) непрерывна на отрезке [ a; b ], причем f(a)=c, f(b)=d, то обратная функция определена и непрерывна на отрезке [ c; d ].
Замечание 2. Если функция y=f(x) не является ни возрастающей, ни убывающей на некотором интервале, то она может иметь несколько обратных функций.
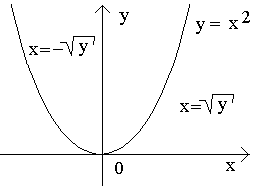 Пример. Функция y=x2 определена при –∞< x <+∞. Она не является ни возрастающей, ни убывающей и не имеет обратной функции. Однако, если мы рассмотрим интервал 0≤ x <+∞, то здесь функция является возрастающей и обратной для нее будет
Пример. Функция y=x2 определена при –∞< x <+∞. Она не является ни возрастающей, ни убывающей и не имеет обратной функции. Однако, если мы рассмотрим интервал 0≤ x <+∞, то здесь функция является возрастающей и обратной для нее будет 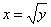 . На интервале – ∞ < x ≤ 0 функция – убывает и обратная для нее
. На интервале – ∞ < x ≤ 0 функция – убывает и обратная для нее 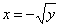 .
.
Замечание 3. Если функции y=f(x) и x=g(y) являются взаимно обратными, то они выражают одну и ту же связь между переменными x и y. Поэтому графикомих является одна и та же кривая. Но если аргумент обратной функции мы обозначим снова через x, а функцию через y и построим их в одной системе координат, то получим уже два различных графика. Легко заметить, что графики будут симметричны относительно биссектрисы 1-го координатного угла.
Дата публикования: 2015-11-01; Прочитано: 560 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
