Напряжения в поперечном сечении

Внутренний сосредоточенный момент 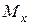, лежащий в плоскости поперечного сечения вала, можно выразить через касательные напряжения, которые, согласно закону Гука, при сдвиге (4.27) связаны с деформацией (4.32)

или, с учетом (4.31), . (4.33)

Тогда элементарный внутренний момент (рис. 4.20) ,

где  площадь элементарной площадки, лежащей в сечении вала на расстоянии от центра тяжести сечения;  элементарная окружная сила.

Суммируя элементарные моменты по площади сечения, получаем выражение для внутреннего сосредоточенного момента ,

или, с учетом выражения (4.33), .

Так как произведение постоянно для всех точек сечения, то .

Интеграл представляет собой геометрическую характеристику поперечного сечения и носит название полярного момента инерции сечения.

Таким образом, , (4.34)

откуда . (4.35)

Произведение называется жесткостью сечения стержня при кручении. Подставим (4.35) в (4.33) и получим выражение для касательного напряжения , (4.36)

из которого следует, что напряжения вдоль радиуса изменяются по линейному закону и наибольшее напряжение при кручении возникает на периферии сечения: ,или где  геометрическая характеристика сечения, которая называется полярным моментом сопротивления.

На рис. 4.21 представлена эпюра касательных напряжений, построенная в соответствии с зависимостью (4.36), для точек, лежащих на диаметре KL. Из эпюры видно, что наиболее нагруженными будут точки, лежащие на максимальном удалении от центра тяжести сечения. В центре тяжести напряжения равны нулю

().