 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Пороговая схема. 2 страница
|
|
9.22. Используя наименьший положительный первообразный корень по модулю  , случайные числа
, случайные числа 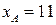 ,
,  , создайте сеансовый ключ для двух пользователей
, создайте сеансовый ключ для двух пользователей  и
и  .
.
9.23. Предложите аналог протокола Диффи-Хеллмена, используя вместо целых чисел квадратные невырожденные матрицы и операцию их умножения.
9.24. Покажите, что модули  пригодны для построения
пригодны для построения  -пороговой схемы разделения секрета. Найдите секрет
-пороговой схемы разделения секрета. Найдите секрет  , если
, если 



 .
.
9.25. Пусть  - различные простые числа. Докажите, что существуют натуральные числа
- различные простые числа. Докажите, что существуют натуральные числа  , такие, что числа
, такие, что числа  пригодны для реализации
пригодны для реализации  -пороговой схемы,
-пороговой схемы,  .
.
9.26. Пусть модули  реализуют
реализуют  -пороговую схему. Докажите, что они также реализуют все
-пороговую схему. Докажите, что они также реализуют все  -пороговые схемы,
-пороговые схемы,  .
.
9.27. Предложите способ генерации модулей для любой  -пороговой схемы.
-пороговой схемы.
Кодирование.
Рассмотрим двоичное кодирование и декодирование, обеспечивающее передачу данных по каналам с “шумом”. Мы будем говорить о вероятности р того, что переданный символ (0 или 1) будет принят правильно и вероятности q = 1 – p того, что переданный символ (0 или 1) будет принят неправильно. При этом предполагается, что ошибки происходят независимо друг от друга. Такая передача данных называется двоичным симметричным каналом. Пусть по двоичному симметричному каналу передается n -битовая последовательность. Вероятность того, что она будет принята ровно с к ошибками, равна 
Двоичным (m, n)-кодом называется пара, состоящая из схемы кодирования  и схемы декодирования
и схемы декодирования  , где
, где  множество всех двоичных последовательностей длины n, причем функции D и E выбираются так, что функция
множество всех двоичных последовательностей длины n, причем функции D и E выбираются так, что функция  является тождественной с вероятностью, близкой к 1. Функции D и E считаются безошибочными, т.е.
является тождественной с вероятностью, близкой к 1. Функции D и E считаются безошибочными, т.е.  является тождественной. Функция Т называется функцией ошибок. Различают два вида кодов:
является тождественной. Функция Т называется функцией ошибок. Различают два вида кодов:
1.коды с исправлением ошибок (цель: восстановить с вероятностью, близкой к 1, переданное сообщение);
2.коды с обнаружением ошибок (цель: выявить с вероятностью, близкой к 1,наличие ошибок).
Примеры двоичных кодов:
1. (m, 3 m)- код с тройным повторением. Сообщение разбивается на блоки длиной m и каждый блок передается трижды. Это определяет функцию Е. Функция D определяется следующим образом: принятая строка разбивается на блоки длиной 3 m. В каждом таком блоке  по тройке символов
по тройке символов  в схеме декодирования восстанавливается символ, чаще всего встречающийся в этой тройке и ставится на i -е место в декодированном блоке.
в схеме декодирования восстанавливается символ, чаще всего встречающийся в этой тройке и ставится на i -е место в декодированном блоке.
2. (m, m + 1)- код с обнаружением ошибок на основе проверки четности. В этом случае функции D и E имеют следующий вид:
 где
где 

Блочный (m, n)-код определяется двумя функциями  и
и  , при этом функция
, при этом функция  является тождественной, чтобы сообщение было принято правильно при отсутствии помех.
является тождественной, чтобы сообщение было принято правильно при отсутствии помех.
Расстоянием Хэмминга между двумя двоичными словами  и
и  называется число позиций, в которых
называется число позиций, в которых  Обозначение:
Обозначение:  Весом слова
Весом слова  называется число единиц среди его координат. Обозначение:
называется число единиц среди его координат. Обозначение:  Несложно проверить, что
Несложно проверить, что 
Свойства расстояния Хэмминга:
1. 
2. 
3.Вероятность того, что слово  будет принято как
будет принято как  равна
равна 
Для того чтобы код давал возможность обнаруживать все ошибки в не более к позициях, необходимо и достаточно, чтобы наименьшее расстояние между кодовыми словами было не меньше k + 1. Для того чтобы код давал возможность исправлять все ошибки в не более к позициях, необходимо и достаточно, чтобы наименьшее расстояние между кодовыми словами было не меньше 2 k + 1.
Если код исправляет не более к ошибок, то вероятность правильного приема слова длины n будет не меньше, чем  Соответственно вероятность неправильного приема слова длины n будет не больше, чем
Соответственно вероятность неправильного приема слова длины n будет не больше, чем 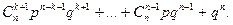
Пусть данное слово  длины кодируется в кодовое слово
длины кодируется в кодовое слово  длины n. Двоичный симметричный канал связи при передаче слово b переводит в слово
длины n. Двоичный симметричный канал связи при передаче слово b переводит в слово  , т.е. добавляет к нему строку ошибок
, т.е. добавляет к нему строку ошибок  а именно,
а именно,  (покомпонентное сложение по модулю 2). Система, обнаруживающая ошибки, проверяет, является ли принятое слово кодовым, и сигнализирует об ошибке, если это не так. Система, исправляющая ошибки, переводит слово
(покомпонентное сложение по модулю 2). Система, обнаруживающая ошибки, проверяет, является ли принятое слово кодовым, и сигнализирует об ошибке, если это не так. Система, исправляющая ошибки, переводит слово  в ближайшее кодовое слово
в ближайшее кодовое слово 
Пусть  некоторая
некоторая  матрица, состоящая из нулей и единиц. Пусть
матрица, состоящая из нулей и единиц. Пусть  (суммирование по модулю 2), т.е.
(суммирование по модулю 2), т.е.  где
где  Эта схема кодирования определяет
Эта схема кодирования определяет  код, называемый матричным кодом, а матрица
код, называемый матричным кодом, а матрица  называется кодирующей матрицей. При матричном кодировании код не должен приписывать одно и то же кодовое слово разным словам. Простой способ добиться этого состоит в том, чтобы первые m столбцов матрицы Е образовывали единичную подматрицу. Если а пробегает множество всех слов длины m, то множество полученных кодовых слов aE образует группу. Два матричных кода называются эквивалентными, если множества кодовых слов совпадают. Пусть
называется кодирующей матрицей. При матричном кодировании код не должен приписывать одно и то же кодовое слово разным словам. Простой способ добиться этого состоит в том, чтобы первые m столбцов матрицы Е образовывали единичную подматрицу. Если а пробегает множество всех слов длины m, то множество полученных кодовых слов aE образует группу. Два матричных кода называются эквивалентными, если множества кодовых слов совпадают. Пусть  - кодирующая матрица, матрица
- кодирующая матрица, матрица  называется проверочной матрицей, если выполняются следующие условия: 1) если размер
называется проверочной матрицей, если выполняются следующие условия: 1) если размер  равен
равен  , то размер
, то размер  равен
равен  ; 2)
; 2)  ; 3) столбцы матрицы
; 3) столбцы матрицы  линейно независимы.
линейно независимы.
Блочный код называется групповым, если его кодовые слова образуют группу. Если код является групповым, то наименьшее расстояние между двумя кодовыми словами равно наименьшему весу ненулевого кодового слова. Схема декодирования исходит из таблицы С всех слов, которые могут быть приняты. Кодовые слова образуют подгруппу В в группе С. Если слово  пробегает все двоичные слова, то мы получаем
пробегает все двоичные слова, то мы получаем  кодовых слов аЕ, а именно,
кодовых слов аЕ, а именно,  т.е.
т.е.  Пусть
Пусть  Рассмотрим множество
Рассмотрим множество  Элемент
Элемент  называется лидером этого класса. Без ограничения общности можно считать, что
называется лидером этого класса. Без ограничения общности можно считать, что  действительно является словом наименьшего веса. Далее находим слово
действительно является словом наименьшего веса. Далее находим слово  наименьшего веса такое, что
наименьшего веса такое, что  Рассмотрим множество
Рассмотрим множество  И так далее продолжаем этот процесс. В результате группу С можно представить в виде объединения классов:
И так далее продолжаем этот процесс. В результате группу С можно представить в виде объединения классов:

Декодирование слова  состоит в выборе кодового слова
состоит в выборе кодового слова  в качестве переданного. Если лидерами являются слова наименьшего веса, то кодовое слово, стоящее в данном столбце, является ближайшим кодовым словом ко всем словам этого столбца.
в качестве переданного. Если лидерами являются слова наименьшего веса, то кодовое слово, стоящее в данном столбце, является ближайшим кодовым словом ко всем словам этого столбца.
Код Хэмминга – это частный случай (m, n)-кода. В этом случае 
 Код Хэмминга строится следующим образом:
Код Хэмминга строится следующим образом:
1. Строим матрицу  размерами
размерами  в i -ой строке которой стоят цифры двоичного представления числа i.
в i -ой строке которой стоят цифры двоичного представления числа i.
2. Записываем систему уравнений bM = O, где  нулевая матрица размерами
нулевая матрица размерами 
3. Чтобы закодировать сообщение a, берем в качестве  соответствующие биты сообщения a и находим с помощью системы bM = O элементы
соответствующие биты сообщения a и находим с помощью системы bM = O элементы 
4. Декодирование кода Хэмминга происходит следующим образом: пусть b – переданное кодовое слово, е – строка ошибок, тогда b + e – принятое слово. Так как bM = O, то (b+е)M = еМ. Если результат нулевой (т.е. (b+е)M =О), как происходит при правильной передаче, то считается, что ошибок не было. Если строка ошибок имеет единицу в i -ой позиции, то еМ – это i -ая строка матрицы М, т.е. двоичное представление числа i, следовательно, ошибка произошла в i -ой позиции, поэтому символ в в i -ой позиции числа b + e следует изменить.
Код называется совершенным, если он способен исправлять все ошибки не более, чем в  разрядах и не способен исправлять никаких ошибок более чем в
разрядах и не способен исправлять никаких ошибок более чем в  разрядах для некоторого натурального
разрядах для некоторого натурального  . Код Хемминга является совершенным кодом.
. Код Хемминга является совершенным кодом.
Пример 10.1. Пусть по двоичному симметричному каналу передаётся слово длины 6 с помощью (2,3)-кода с обнаружением ошибок на основе проверки четности. Найти вероятность  того, что при приёме сообщения ошибка не будет обнаружена при условии, что ошибка произошла, если вероятность ошибочного приема одного символа равна
того, что при приёме сообщения ошибка не будет обнаружена при условии, что ошибка произошла, если вероятность ошибочного приема одного символа равна  .
.
Решение. При передаче сообщение длины 6 разбивается на три сообщения длины 2:  ,
,  ,
,  , где
, где  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  . Обозначим через
. Обозначим через  событие, состоящее в том, что при передаче сообщения произошла ошибка, через
событие, состоящее в том, что при передаче сообщения произошла ошибка, через  обозначим событие, состоящее в том, что при приёме не обнаружена ошибка. Тогда
обозначим событие, состоящее в том, что при приёме не обнаружена ошибка. Тогда  . Очевидно,
. Очевидно,  , где
, где 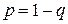 . Допущенная ошибка не будет обнаружена лишь в том случае, когда при передаче каждой из групп символов
. Допущенная ошибка не будет обнаружена лишь в том случае, когда при передаче каждой из групп символов  ,
,  , число допущенных ошибок равно 0 или 2, при этом хотя бы в одном из блоков
, число допущенных ошибок равно 0 или 2, при этом хотя бы в одном из блоков  произошло 2 ошибки. Вероятность ошибки в двух символах при передаче группы символов
произошло 2 ошибки. Вероятность ошибки в двух символах при передаче группы символов  равна
равна  . Поэтому
. Поэтому  . Таким образом,
. Таким образом,  .
.
Ответ:  .
.
Пример 10.2. Пусть по двоичному симметричному каналу передаются слова и вероятность ошибочного приема одного символа равна  . Найти вероятность
. Найти вероятность  необнаруженной ошибки в одном символе при использовании (m, 3m) -кода с тройным повторением.
необнаруженной ошибки в одном символе при использовании (m, 3m) -кода с тройным повторением.
Решение. Обозначим через  событие, состоящее в том, что при передаче символа
событие, состоящее в том, что при передаче символа  произошла ошибка, через
произошла ошибка, через  обозначим событие, состоящее в том, что при приёме не обнаружена ошибка. Очевидно,
обозначим событие, состоящее в том, что при приёме не обнаружена ошибка. Очевидно, 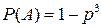 , где
, где 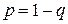 . Произошедшая ошибка не будет обнаружена, если символ
. Произошедшая ошибка не будет обнаружена, если символ  принят дважды неправильно или трижды неправильно. Поэтому
принят дважды неправильно или трижды неправильно. Поэтому  . Следовательно,
. Следовательно,
 .
.
Ответ:  .
.
Пример 10.3. Какие ошибки обнаруживает и какие ошибки исправляет следующий блочный (2,5)-код:  ,
,  ,
, 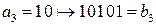 ,
,  ?
?
Решение. Найдем расстояния Хемминга между кодовыми словами: 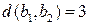 ,
,  ,
,  ,
,  ,
,  ,
,  . Так как расстояние Хемминга между различными кодовыми словами не меньше 3, то рассматриваемый код обнаруживает ошибки, допущенные в двух разрядах, и исправляет ошибки, допущенные в одном разряде.
. Так как расстояние Хемминга между различными кодовыми словами не меньше 3, то рассматриваемый код обнаруживает ошибки, допущенные в двух разрядах, и исправляет ошибки, допущенные в одном разряде.
Ответ: код обнаруживает ошибки в двух разрядах и исправляет ошибки в одном разряде.
Пример 10.4. Проверить, что двоичный код с матрицей  является групповым. Построить схему декодирования, используя в качестве лидеров смежных классов слова наименьшего веса.
является групповым. Построить схему декодирования, используя в качестве лидеров смежных классов слова наименьшего веса.
Решение. Схема кодирования выглядит следующим образом:
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 ,
,
 .
.
Проверим, что множество  кодовых слов образует абелеву группу относительно побитового сложения. Так как
кодовых слов образует абелеву группу относительно побитового сложения. Так как  , то для любых
, то для любых 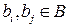 имеем
имеем  . Очевидно, операция побитового сложения коммутативна. Нейтральным элементов множества
. Очевидно, операция побитового сложения коммутативна. Нейтральным элементов множества  является слово
является слово  . Докажем, что для любого слова
. Докажем, что для любого слова  существует слово
существует слово  , такое, что
, такое, что  . Так как множество
. Так как множество  образует абелеву группу относительно побитового сложения, то для любого слова
образует абелеву группу относительно побитового сложения, то для любого слова  существует
существует  , такое, что
, такое, что  . Следовательно,
. Следовательно,  . Таким образом, матрица
. Таким образом, матрица  определяет групповой код.
определяет групповой код.
Построим схему декодирования, выбрав в качестве лидеров смежных классов слова из  наименьшего веса:
наименьшего веса:
| 000001 | 010010 | 101000 | |||||
| 000010 | 010001 | 100100 | |||||
| 000100 | 011000 | 100010 | |||||
| 001000 | 010100 | 100001 | |||||
| 010000 | 000011 | 001100 | |||||
| 100000 | 000110 | 001001 | |||||
| 000101 |
Так как  ,
,  , то
, то  . Следовательно, мы должны выбрать 8 лидеров смежных классов. Выберем все слова веса 0 и 1:
. Следовательно, мы должны выбрать 8 лидеров смежных классов. Выберем все слова веса 0 и 1:  . Выберем любое слово
. Выберем любое слово  веса 2, которое не содержится во множестве слов
веса 2, которое не содержится во множестве слов  ,
,  ,
,  . Множество всех слов из
. Множество всех слов из  разбивается на смежные классы
разбивается на смежные классы  ,
,  . В первом столбце таблицы указаны лидеры смежных классов
. В первом столбце таблицы указаны лидеры смежных классов  ,
,  , в первой строке таблицы – кодовые слова
, в первой строке таблицы – кодовые слова  ,
,  . Чтобы декодировать принятое слово
. Чтобы декодировать принятое слово  следует отыскать его в таблице и выбрать в качестве переданного кодовое слово в том же столбце и первой строке. Например, если принято слово 110011, считается, что было передано слово 010011; если принято 110101, считается, что оно и было передано и т.п. Построенный код исправляет все одинарные ошибки, а также двойную ошибку 000101.
следует отыскать его в таблице и выбрать в качестве переданного кодовое слово в том же столбце и первой строке. Например, если принято слово 110011, считается, что было передано слово 010011; если принято 110101, считается, что оно и было передано и т.п. Построенный код исправляет все одинарные ошибки, а также двойную ошибку 000101.
Пример 10.5. Для передачи двоичных слов длины 4 был использован (4,7)-код Хемминга. Известно, что при передаче слова была допущена ошибка в одном разряде. Определите, какое слово передавалось, если получено сообщение  =0011111.
=0011111.
Дата публикования: 2015-11-01; Прочитано: 570 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
