 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Пороговая схема. 1 страница
|
|
Будем говорить, что t участников  (законных пользователей) к -хранят секрет с (
(законных пользователей) к -хранят секрет с ( ), если
), если
1.каждый  знает некоторую информацию (частичный секрет)
знает некоторую информацию (частичный секрет)  неизвестную любому другому участнику;
неизвестную любому другому участнику;
2.секрет с может быть легко вычислен на основе любых к частичных секретов 
3.знание любых к – 1 частичных секретов не дает такой возможности.
Множество  , удовлетворяющее этим условиям, называется (к,t)-пороговой схемой.
, удовлетворяющее этим условиям, называется (к,t)-пороговой схемой.
Приведем способ построения пороговой схемы на основе теории сравнений.
Пусть зафиксированы числа к, t ( ).
).
Пусть  различные натуральные попарно взаимно простые числа (
различные натуральные попарно взаимно простые числа ( ).
).
Обозначим через  наименьшее произведение k различных модулей, а через
наименьшее произведение k различных модулей, а через 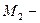 наибольшее произведение к – 1 различных модулей, т.е.
наибольшее произведение к – 1 различных модулей, т.е. 

Модули  следует выбирать так, чтобы
следует выбирать так, чтобы 
Случайным образом выберем число с такое, что 
В качестве секретов участников 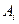 возьмем наименьшие неотрицательные вычеты секрета с по модулям
возьмем наименьшие неотрицательные вычеты секрета с по модулям  , т.е.
, т.е. 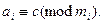
Каждому участнику 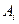 сообщаем
сообщаем 
Построенное выше множество  является (к,t)-пороговой схемой.
является (к,t)-пороговой схемой.
Пример 1. Предположим, что абоненты  и
и  решили установить скрытую связь без передачи ключей. Для этого абоненты выбрали простое число
решили установить скрытую связь без передачи ключей. Для этого абоненты выбрали простое число  , абонент А выбирает секретный ключ
, абонент А выбирает секретный ключ  , абонент
, абонент  выбирает секретный ключ
выбирает секретный ключ  . Осуществить передачу сообщения
. Осуществить передачу сообщения  от абонента
от абонента  абоненту
абоненту  .
.
Решение. Абонент  , решая сравнение
, решая сравнение  , находит свой второй секретный ключ
, находит свой второй секретный ключ 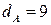 ; абонент
; абонент  , решая сравнение
, решая сравнение 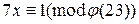 , находит свой второй секретный ключ
, находит свой второй секретный ключ  . Затем абонент
. Затем абонент  шифрует сообщение
шифрует сообщение  своим первым секретным ключом и передаёт шифрованное сообщение абоненту
своим первым секретным ключом и передаёт шифрованное сообщение абоненту  :
:  . Абонент
. Абонент  , получив сообщение
, получив сообщение  , шифрует его своим первым секретным ключом и передаёт абоненту
, шифрует его своим первым секретным ключом и передаёт абоненту  :
:  . Абонент
. Абонент  шифрует сообщение
шифрует сообщение 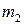 своим вторым секретным ключом и передает абоненту
своим вторым секретным ключом и передает абоненту  :
: 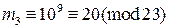 . Получив это сообщение, абонент
. Получив это сообщение, абонент  расшифровывает его при помощи своего второго ключа:
расшифровывает его при помощи своего второго ключа:  .
.
Пример 2. Предположим, что абоненты  и
и  решили установить скрытую связь с открытым ключом. Пусть
решили установить скрытую связь с открытым ключом. Пусть 
 - простые числа абонента
- простые числа абонента  ,
,  ,
,  - простые числа абонента
- простые числа абонента  , телефонные книги абонентов
, телефонные книги абонентов  и
и  имеют вид:
имеют вид:  ,
,  ;
;  ,
,  . Осуществить передачу секретного сообщения
. Осуществить передачу секретного сообщения  от абонента
от абонента  к абоненту
к абоненту  и секретного сообщения
и секретного сообщения  от абонента
от абонента  к абоненту
к абоненту  .
.
Решение. Решая сравнение 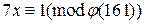 , абонент
, абонент  находит секретный ключ
находит секретный ключ  . Решая сравнение
. Решая сравнение  , абонент
, абонент  находит секретный ключ
находит секретный ключ  . Абонент
. Абонент  шифрует сообщение
шифрует сообщение  открытым ключом абонента
открытым ключом абонента  и отправляет шифрованное сообщение абоненту
и отправляет шифрованное сообщение абоненту  :
:  . Получив сообщение
. Получив сообщение  , абонент
, абонент  расшифровывает его своим секретным ключом:
расшифровывает его своим секретным ключом:  . Абонент
. Абонент  шифрует сообщение
шифрует сообщение  открытым ключом абонента
открытым ключом абонента  и отправляет зашифрованное сообщение абоненту
и отправляет зашифрованное сообщение абоненту  :
: 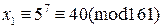 . Далее абонент
. Далее абонент  расшифровывает полученное сообщение
расшифровывает полученное сообщение  своим секретным ключом:
своим секретным ключом:  .
.
Пример 3. Предположим, что абоненты  и
и  решили установить скрытую связь с открытым ключом с электронной подписью. Пусть
решили установить скрытую связь с открытым ключом с электронной подписью. Пусть 
 - простые числа абонента
- простые числа абонента  ,
,  ,
,  - простые числа абонента
- простые числа абонента  , телефонные книги абонентов
, телефонные книги абонентов  и
и  имеют вид:
имеют вид:  ,
,  ;
;  ,
,  . Осуществить передачу сообщения
. Осуществить передачу сообщения  с электронной подписью от абонента
с электронной подписью от абонента  к абоненту
к абоненту  .
.
Решение. Решая сравнения  и
и  , абоненты
, абоненты  и
и  находят свои секретные ключи
находят свои секретные ключи  ,
,  . Так как
. Так как  , то абонент
, то абонент  сначала шифрует сообщение
сначала шифрует сообщение  открытым ключом абонента
открытым ключом абонента  :
:  , а затем шифрует сообщение
, а затем шифрует сообщение  своим секретным ключом:
своим секретным ключом:  и отправляет сообщение
и отправляет сообщение 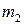 абоненту
абоненту  . Абонент
. Абонент  получив сообщение
получив сообщение 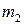 сначала расшифровывает его открытым ключом абонента
сначала расшифровывает его открытым ключом абонента  :
:  , а затем расшифровывает сообщение
, а затем расшифровывает сообщение  своим секретным ключом:
своим секретным ключом:  .
.
Пример 4. Используя наименьший положительный первообразный корень по модулю  и случайные числа
и случайные числа  ,
,  , создайте сеансовый ключ для двух пользователей
, создайте сеансовый ключ для двух пользователей  и
и  .
.
Решение. Наименьшим первообразным корнем по модулю  является число
является число  . Пользователь
. Пользователь  выбирает случайное число
выбирает случайное число  , вычисляет
, вычисляет  и отправляет сообщение
и отправляет сообщение 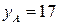 абоненту
абоненту  . Абонент
. Абонент  выбирает случайное число
выбирает случайное число  , вычисляет
, вычисляет  и отправляет сообщение
и отправляет сообщение  абоненту
абоненту  . Далее абонент
. Далее абонент  вычисляет
вычисляет  , абонент
, абонент  вычисляет
вычисляет  . Число
. Число 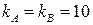 является общим ключом абонентов
является общим ключом абонентов  и
и  .
.
Ответ: 10.
Пример 5. Проверьте, что модули 

 ,
,  ,
,  и частичные секреты
и частичные секреты  ,
,  ,
,  ,
,  ,
,  образуют (3,5)-пороговую схему, а также найдите секрет
образуют (3,5)-пороговую схему, а также найдите секрет  .
.
Решение. Так как  , то модули
, то модули  ,
,  , пригодны для реализации пороговой схемы. Система сравнений
, пригодны для реализации пороговой схемы. Система сравнений 

 имеет единственное решение
имеет единственное решение  . Кроме того,
. Кроме того,  для любого
для любого  . Знание каких-либо двух частичных секретов
. Знание каких-либо двух частичных секретов  не позволяет восстановить секрет
не позволяет восстановить секрет  . Следовательно, множество
. Следовательно, множество  образует (3,5)-пороговую схему.
образует (3,5)-пороговую схему.
Ответ:  .
.
9.1. Применить модулярное шифрование  к словам ALGEBRA и NUMBER, отождествляя латинский алфавит с
к словам ALGEBRA и NUMBER, отождествляя латинский алфавит с  , если:
, если:
1) 
2)  .
.
9.2. Найти обратные преобразования к шифрам из предыдущей задачи и применить их для дешифрования.
9.3. Объясните необходимость условия  при модулярном шифровании
при модулярном шифровании  .
.
9.4. Покажите, что композиция двух модулярных шифров 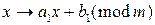 ,
,  , где
, где  , будет снова модулярным шифром.
, будет снова модулярным шифром.
9.5. Как обратить композицию двух модулярных шифров  ?
?
9.6. Пусть  :
: 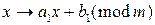 ,
,  :
:  - модулярные шифры. Найдите все значения параметров
- модулярные шифры. Найдите все значения параметров  , для которых
, для которых  .
.
9.7. Отождествляя латинский алфавит с  и применяя RSA-шифрование с параметрами
и применяя RSA-шифрование с параметрами  ,
, 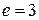 , зашифровать слова ALGEBRA и NUMBER и дешифровать сообщение «17, 26, 12, 12, 9».
, зашифровать слова ALGEBRA и NUMBER и дешифровать сообщение «17, 26, 12, 12, 9».
9.8. Приняв 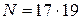 ,
,  , зашифруйте сообщение
, зашифруйте сообщение  . Путем дешифрования убедитесь в корректности работы RSA-криптосистемы с выбранными параметрами. Используйте RSA-криптосистему для подписи сообщения и проверьте его подлинность.
. Путем дешифрования убедитесь в корректности работы RSA-криптосистемы с выбранными параметрами. Используйте RSA-криптосистему для подписи сообщения и проверьте его подлинность.
9.9. Вычислите секретный ключ для открытого ключа  в следующих двух случаях:
в следующих двух случаях:  ,
,  .
.
9.10. Пусть  и
и  - взаимно обратные RSA-преобразования. Покажите, что
- взаимно обратные RSA-преобразования. Покажите, что  для любого
для любого  , а не только для
, а не только для  .
.
9.11. Докажите, что RSA-преобразования при фиксированном  образуют группу относительно операции их композиции.
образуют группу относительно операции их композиции.
9.12. Обосновать нестойкость RSA-криптосистемы, если по ошибке вместо  взяли
взяли  .
.
9.13. Показать, что кроме двух очевидных решений  сравнение
сравнение  имеет еще два решения
имеет еще два решения  ,
,  .
.
9.14. Покажите, что, зная  , легко факторизовать RSA-модуль
, легко факторизовать RSA-модуль  .
.
9.15. Подпишите сообщение  и проверьте подлинность, если
и проверьте подлинность, если 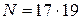 ,
,  .
.
9.16. Покажите, что сообщение  является неподвижным (
является неподвижным ( ) в RSA-криптосистеме с параметрами
) в RSA-криптосистеме с параметрами 
 Найдите все неподвижные сообщения.
Найдите все неподвижные сообщения.
9.17. Покажите, что в RSA-криптосистеме с параметрами 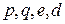 имеется
имеется  неподвижных сообщений
неподвижных сообщений  ,
,  , где
, где 
 .
.
9.18. Пусть  . Зашифруйте сообщение
. Зашифруйте сообщение  по системе Рабина. Путем дешифрования убедитесь в корректности работы криптосистемы Рабина с выбранными параметрами.
по системе Рабина. Путем дешифрования убедитесь в корректности работы криптосистемы Рабина с выбранными параметрами.
9.19. Предположим, что абоненты  и
и  решили установить секретную переписку с использованием системы Рабина. Для этого они выбрали простые числа
решили установить секретную переписку с использованием системы Рабина. Для этого они выбрали простые числа  вида
вида  , модуль
, модуль  и договорились, что будут обмениваться лишь такими сообщениями
и договорились, что будут обмениваться лишь такими сообщениями  , для которых
, для которых  и
и  является квадратичным вычетом по модулям
является квадратичным вычетом по модулям 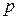 и
и  . Докажите, что в этом случае дешифрование осуществляется однозначно.
. Докажите, что в этом случае дешифрование осуществляется однозначно.
9.20. Пусть  , где
, где  - различные простые числа вида
- различные простые числа вида  . Доказать эквивалентность условий:
. Доказать эквивалентность условий:
1) существует эффективный алгоритм решения сравнения  ;
;
2) существует эффективный алгоритм факторизации модуля  .
.
9.21. Пусть  ,
,  , где
, где  - различные простые числа. Доказать, что если сравнение
- различные простые числа. Доказать, что если сравнение  имеет одно решение, то оно имеет четыре решения на промежутке
имеет одно решение, то оно имеет четыре решения на промежутке  .
.
Дата публикования: 2015-11-01; Прочитано: 555 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
