 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Показательные и полиномиальные сравнения. 4 страница
|
|
Пример 2. В кольце многочленов с действительными коэффициентами  найдите идеал, порождённый множеством
найдите идеал, порождённый множеством  .
.
Решение. Докажем, что  . С одной стороны, так как
. С одной стороны, так как  , то любой элемент идеала
, то любой элемент идеала 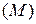 делится на многочлен
делится на многочлен  . С другой стороны, так как
. С другой стороны, так как  , то для любого многочлена
, то для любого многочлена  существуют многочлены
существуют многочлены  ,
,  , такие, что
, такие, что  . Следовательно,
. Следовательно,  .
.
Пример 3. Найдите число гомоморфизмов из кольца  в кольцо
в кольцо  .
.
Решение. Пусть j: Z 40® Z 60 – гомоморфизм, тогда j (0)=0. Возьмём произвольное  , тогда
, тогда  . Очевидно, что любое отображение вида:
. Очевидно, что любое отображение вида:  является гомоморфизмом из
является гомоморфизмом из  в
в  тогда и только тогда, когда
тогда и только тогда, когда  . Таким образом, искомое число гомоморфизмов равняется числу вычетов
. Таким образом, искомое число гомоморфизмов равняется числу вычетов 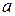 в полной системе вычетов, удовлетворяющих сравнению
в полной системе вычетов, удовлетворяющих сравнению  . Так как
. Так как  , то каждое решение рассматриваемого сравнения удовлетворяет системе:
, то каждое решение рассматриваемого сравнения удовлетворяет системе:

где  ,
,  . Верно и обратное, каждое решение системы является решением сравнения. При фиксированных
. Верно и обратное, каждое решение системы является решением сравнения. При фиксированных 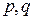 система имеет единственное решение в полной системе вычетов по модулю 60. Так как
система имеет единственное решение в полной системе вычетов по модулю 60. Так как  , то количество пар чисел
, то количество пар чисел 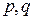 , удовлетворяющих условиям
, удовлетворяющих условиям  ,
,  , равняется
, равняется  . Число гомоморфизмов из кольца
. Число гомоморфизмов из кольца  в кольцо
в кольцо  равняется 12.
равняется 12.
7.1. Определите, какие из указанных множеств образуют кольцо относительно заданных операций:
1)  , где
, где  - одно из множеств
- одно из множеств 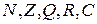 ;
;
2)  , где
, где  - заданное множество;
- заданное множество;
3) 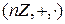 , где
, где 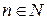 ;
;
4) множество чисел вида  ,
,  , относительно сложения и умножения;
, относительно сложения и умножения;
5) множество  гауссовых чисел
гауссовых чисел  ,
,  , относительно сложения и умножения;
, относительно сложения и умножения;
6) множество вещественных ортогональных матриц порядка 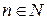 относительно сложения и умножения матриц;
относительно сложения и умножения матриц;
7) множество матриц вида  ,
, 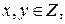 где
где 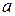 - фиксированное целое число, относительно сложения и умножения матриц;
- фиксированное целое число, относительно сложения и умножения матриц;
8) множество вещественных матриц порядка  , у которых последние две строки нулевые;
, у которых последние две строки нулевые;
9) 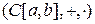 ;
;
10)  ;
;
11) множество функций вещественной переменной, обращающихся в 0 на фиксированном подмножестве  , относительно сложения и умножения.
, относительно сложения и умножения.
7.2. Найдите все подкольца кольца 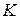 , если:
, если:
1)  ;
;
2) 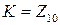 ;
;
3)  ;
;
4)  .
.
7.3. Найдите идеал кольца 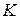 , порождённый множеством
, порождённый множеством  , если:
, если:
1)  ,
,  ;
;
2)  ,
,  ;
;
3) 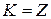 ,
,  ;
;
4)  ,
, 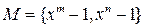 , где
, где  .
.
7.4. Найдите все обратимые элементы в кольцах:
1) вещественных верхних треугольных матриц порядка 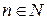 ;
;
2) 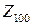 ;
;
3)  .
.
7.5. Найдите число гомоморфизмов из кольца  в кольцо
в кольцо  , если:
, если:
1)  ,
,  ;
;
2)  ,
,  ;
;
3)  ,
,  .
.
7.6. Докажите, что любой идеал кольца  является главным.
является главным.
7.7. Приведите пример кольца без единицы.
7.8. Докажите, что кольцо 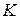 является евклидовым, если:
является евклидовым, если:
1) 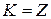 ;
;
2)  ;
;
3)  .
.
7.9. Вычислить фактор-кольца  , если:
, если:
1)  ,
,  ;
;
2) 
 ;
;
3) 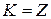 ,
, 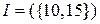 ;
;
4) 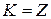 ,
,  , где
, где  - различные натуральные числа.
- различные натуральные числа.
7.10. Докажите, что если  есть идеал кольца
есть идеал кольца 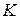 , то
, то  есть идеал кольца
есть идеал кольца  .
.
7.11. Является ли  областью целостности?
областью целостности?
7.12. Найдите все гомоморфизмы из кольца  в кольцо
в кольцо 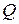 .
.
7.13. Пусть  . Докажите, что отображение
. Докажите, что отображение  , действующее по правилу
, действующее по правилу  , является гомоморфизмом колец
, является гомоморфизмом колец  . Найдите его ядро, образ и фактор-кольцо
. Найдите его ядро, образ и фактор-кольцо  .
.
7.14. Образуют ли идеал необратимые элементы кольца 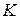 , если:
, если:
1) 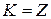 ;
;
2)  ;
;
3)  , где
, где 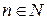 .
.
7.15. Докажите, что кольца  и
и  изоморфны, если:
изоморфны, если:
1)  ,
,  ;
;
2)  ,
,  , где
, где  ;
;
3)  ,
,  , где
, где  - множество всех многочленов с чётными свободными членами в кольце
- множество всех многочленов с чётными свободными членами в кольце 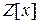 .
.
Поля.
Коммутативное кольцо Р с единицей, состоящее не менее чем из двух элементов, в котором каждый ненулевой элемент обратим, называется полем.
Ясно, что если коммутативное кольцо 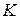 с единицей (
с единицей ( ) не содержит нетривиальных идеалов, то
) не содержит нетривиальных идеалов, то 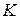 является полем.
является полем.
Если Р – поле, то множество  образует аддитивную абелеву группу, множество
образует аддитивную абелеву группу, множество  образует мультипликативную абелеву группу. В поле нет делителей нуля.
образует мультипликативную абелеву группу. В поле нет делителей нуля.
Подмножество F поля Р называется подполем поля Р, если F само является полем относительно индуцированных операций из поля Р. В этом случае поле P называется расширением поля F.
Пусть 1 – единица поля Р. Наименьшее натуральное число р, для которого  т.е.
т.е.  (р раз), называется характеристикой поля Р (обозначение: char P). Если такого числа р не существует, то говорят, что поле Р имеет нулевую характеристику. Если натуральное число р является характеристикой поля Р, то р является простым числом.
(р раз), называется характеристикой поля Р (обозначение: char P). Если такого числа р не существует, то говорят, что поле Р имеет нулевую характеристику. Если натуральное число р является характеристикой поля Р, то р является простым числом.
Пусть F – расширение поля Р. Система элементов  из
из 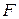 называется линейно зависимой над полем
называется линейно зависимой над полем  , если существуют элементы
, если существуют элементы  , не все из которых нулевые, такие, что
, не все из которых нулевые, такие, что  . Если равенство
. Если равенство  выполняется лишь при
выполняется лишь при  , то система
, то система  называется линейно независимой над полем
называется линейно независимой над полем  . Поле F называется конечным расширением поля P, если F – расширение поля Р и существует линейно независимая над полем
. Поле F называется конечным расширением поля P, если F – расширение поля Р и существует линейно независимая над полем  система
система  из
из 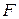 , такая, что любой элемент
, такая, что любой элемент  можно единственным образом представить в виде
можно единственным образом представить в виде  где
где  . В таком случае система
. В таком случае система  называется базисом поля
называется базисом поля 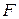 над полем
над полем  . Число элементов базиса F над Р, называется степенью расширения и обозначается
. Число элементов базиса F над Р, называется степенью расширения и обозначается  Если F – конечное расширение поля Р, Т – конечное расширение поля F, то Т – конечное расширение поля Р, причем [ T: P ]=[ T: F ]·[ F: P ].
Если F – конечное расширение поля Р, Т – конечное расширение поля F, то Т – конечное расширение поля Р, причем [ T: P ]=[ T: F ]·[ F: P ].
Многочлен 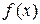 положительной степени с коэффициентами из поля
положительной степени с коэффициентами из поля  называется приводимым над полем
называется приводимым над полем  , если существуют многочлены
, если существуют многочлены 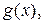
 , такие, что
, такие, что  и
и  . В противном случае многочлен
. В противном случае многочлен 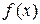 положительной степени называется неприводимым над полем
положительной степени называется неприводимым над полем  .
.
Пусть F – расширение поля Р. Элемент 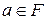 называется алгебраическим над полем Р, если существует многочлен
называется алгебраическим над полем Р, если существует многочлен  такой, что
такой, что  . Расширение F поля Р называется алгебраическим расширением поля Р, если любой элемент поля F является алгебраическим над Р. Минимальным многочленом алгебраического элемента
. Расширение F поля Р называется алгебраическим расширением поля Р, если любой элемент поля F является алгебраическим над Р. Минимальным многочленом алгебраического элемента 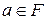 над полем Р называется многочлен
над полем Р называется многочлен 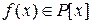 наименьшей степени, для которого
наименьшей степени, для которого  . Минимальный многочлен определён однозначно с точностью до умножения его на ненулевой элемент поля
. Минимальный многочлен определён однозначно с точностью до умножения его на ненулевой элемент поля  и является неприводимым над полем
и является неприводимым над полем  . Если
. Если 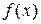 - минимальный многочлен элемента
- минимальный многочлен элемента 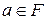 над полем
над полем  и
и  - многочлен, одним из корней которого является элемент
- многочлен, одним из корней которого является элемент 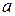 , то многочлен
, то многочлен  делится на многочлен
делится на многочлен 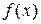 . Степенью алгебраического элемента
. Степенью алгебраического элемента 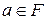 над полем
над полем  называется число, равное степени минимального многочлена элемента
называется число, равное степени минимального многочлена элемента 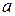 . Элемент
. Элемент  , который является алгебраическим над полем
, который является алгебраическим над полем 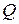 , называется алгебраическим числом.
, называется алгебраическим числом.
Пусть 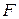 - расширение поля
- расширение поля  . Обозначим через
. Обозначим через  наименьшее поле, содержащее поле
наименьшее поле, содержащее поле  и элемент
и элемент  . Переход от поля
. Переход от поля  к полю
к полю  называется присоединением к
называется присоединением к  элемента
элемента 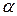 , поле
, поле  называется простым расширением поля
называется простым расширением поля  . Если элемент
. Если элемент 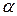 является алгебраическим степени
является алгебраическим степени 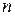 над полем
над полем  , то P [ a ]={ b 0+ b 1a+…+ bn -1 an -1| b 0,…, bn -1Î P } и
, то P [ a ]={ b 0+ b 1a+…+ bn -1 an -1| b 0,…, bn -1Î P } и  . Расширение F поля Р называется полем разложения многочлена
. Расширение F поля Р называется полем разложения многочлена  если
если  в F [ x ], причем F – наименьшее поле, содержащее Р и
в F [ x ], причем F – наименьшее поле, содержащее Р и  . Очевидно, поле разложения многочлена
. Очевидно, поле разложения многочлена  может быть получено последовательным присоединением корней
может быть получено последовательным присоединением корней  ,
,  , многочлена
, многочлена 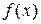 .
.
Если F – конечное поле с единицей 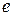 , то F содержит
, то F содержит 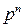 элементов, где
элементов, где 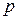 - характеристика поля F,
- характеристика поля F, 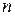 - степень расширения поля F над полем
- степень расширения поля F над полем  .
.
Кольцо вычетов  является полем тогда и только тогда, когда m является простым числом.
является полем тогда и только тогда, когда m является простым числом.
Пусть  - поле, фактор-кольцо
- поле, фактор-кольцо  является полем тогда и только тогда, когда многочлен
является полем тогда и только тогда, когда многочлен 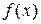 неприводим над полем
неприводим над полем  .
.
Отметим, что неприводимыми над полем  являются лишь многочлены первой степени, неприводимыми над полем
являются лишь многочлены первой степени, неприводимыми над полем 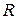 являются многочлены первой степени и многочлены второй степени, не имеющие действительных корней. Достаточное условие неприводимости многочлена над полем
являются многочлены первой степени и многочлены второй степени, не имеющие действительных корней. Достаточное условие неприводимости многочлена над полем 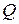 даёт следующий признак Эйзенштейна: пусть
даёт следующий признак Эйзенштейна: пусть  - многочлен с целыми коэффициентами положительной степени
- многочлен с целыми коэффициентами положительной степени 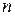 и существует простое число
и существует простое число 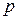 , такое, что числа
, такое, что числа  делятся на
делятся на 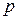 , число
, число  не делится на
не делится на 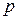 , число
, число  делится на
делится на 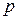 , но не делится на
, но не делится на  , тогда многочлен
, тогда многочлен 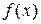 неприводим над полем
неприводим над полем 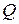 .
.
Пример 1. Пусть  - произвольное поле. Определите, образует ли поле множество
- произвольное поле. Определите, образует ли поле множество  , состоящее из рациональных функций
, состоящее из рациональных функций  , где
, где 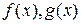 - взаимно простые многочлены над полем
- взаимно простые многочлены над полем  ,
,  .
.
Решение. Множество  образует абелеву группу относительно операции сложения функций. Умножение функций ассоциативно и коммутативно, выполняется закон дистрибутивности относительно сложения и умножения. Следовательно, множество
образует абелеву группу относительно операции сложения функций. Умножение функций ассоциативно и коммутативно, выполняется закон дистрибутивности относительно сложения и умножения. Следовательно, множество  образует коммутативное кольцо. Функция
образует коммутативное кольцо. Функция  является единицей кольца. Для любой функции
является единицей кольца. Для любой функции  элемент
элемент 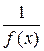 принадлежит множеству
принадлежит множеству  и является обратным элементом для
и является обратным элементом для 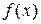 . Учитывая, что
. Учитывая, что  , заключаем, что множество
, заключаем, что множество  образует поле.
образует поле.
Дата публикования: 2015-11-01; Прочитано: 1149 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
