 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Показательные и полиномиальные сравнения. 3 страница
|
|
6)  , где
, где 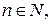
 - множество целых чисел, кратных
- множество целых чисел, кратных 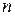 ;
;
7)  ;
;
8) множество  относительно операции
относительно операции  :
: 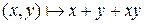 ;
;
9) множество всех комплексных корней  из 1 фиксированной степени
из 1 фиксированной степени 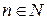 относительно умножения;
относительно умножения;
10) множество всех комплексных корней  из 1 произвольных степеней относительно умножения;
из 1 произвольных степеней относительно умножения;
11) множество всех комплексных чисел с фиксированным модулем  относительно умножения;
относительно умножения;
12) множество всех комплексных чисел с ненулевыми рациональными модулями относительно умножения;
13) положительные действительные числа относительно операции  ;
;
14) целочисленные матрицы порядка 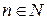 с определителем, равным 1, относительно умножения;
с определителем, равным 1, относительно умножения;
15) невырожденные квадратные матрицы порядка 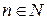 с элементами из множества
с элементами из множества  относительно умножения, где
относительно умножения, где  - одно из множеств
- одно из множеств  ;
;
16)  , где
, где  - множество классов вычетов по модулю
- множество классов вычетов по модулю 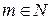 , кратных
, кратных 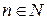 , причем n делитель m;
, причем n делитель m;
17)  , где
, где  , причем n делитель m;
, причем n делитель m;
18)  , где множество
, где множество  состоит из классов вычетов по модулю
состоит из классов вычетов по модулю 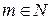 , взаимно простых с
, взаимно простых с  ;
;
19)  , где
, где  - множество всех подмножеств заданного множества
- множество всех подмножеств заданного множества  ,
,  - операция симметрической разности множеств;
- операция симметрической разности множеств;
20)  , где
, где  - фиксированное действительное число.
- фиксированное действительное число.
6.2. Определите, являются ли изоморфными указанные группы:
1)  и
и  ;
;
2) 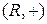 и
и  ;
;
3)  и
и  ;
;
4)  и
и  , где
, где 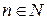 ;
;
5) группа мономиальных матриц  порядка
порядка 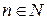 относительно умножения и группа подстановок
относительно умножения и группа подстановок  ;
;
6)  и
и  .
.
6.3. Найдите все, с точностью до изоморфизма, группы порядков 2 и 3.
6.4. Приведите пример двух неизоморфных групп одинакового конечного порядка.
6.5. Описать левые смежные классы группы  по подгруппе
по подгруппе  в следующих случаях:
в следующих случаях:
1) 
 ;
;
2)  ,
,  ;
;
3)  ,
,  , где
, где  ,
,  - множество всех невырожденных матриц порядка
- множество всех невырожденных матриц порядка 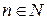 с действительными коэффициентами и множество матриц порядка
с действительными коэффициентами и множество матриц порядка 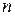 с действительными коэффициентами и определителем, равным 1.
с действительными коэффициентами и определителем, равным 1.
6.6. Найдите все подгруппы группы  и укажите среди них нормальные, если:
и укажите среди них нормальные, если:
1)  ;
;
2)  - циклическая группа 12-го порядка;
- циклическая группа 12-го порядка;
3)  .
.
6.7. Докажите, что в конечной группе нечётного порядка имеется однозначно определенная операция извлечения квадратного корня.
6.8. Докажите, что всякая группа простого порядка является циклической.
6.9. Докажите, что подгруппа индекса 2 в любой группе является нормальной.
6.10. Докажите, что в любой конечной группе чётного порядка есть элемент порядка 2.
6.11. Сколько элементов порядка 6 имеет группа  , если:
, если:
1)  ;
;
2) 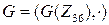 ;
;
3)  .
.
6.12. Найти порядок указанного элемента 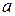 в группе
в группе  , если:
, если:
1)  ,
,  ;
;
2)  ,
,  ;
;
3)  ,
,  ;
;
4)  ,
,  , где
, где  .
.
6.13. Вычислите  в группе
в группе  , если:
, если:
1)  ,
,  ;
;
2)  ,
,  ;
;
3)  ,
,  .
.
6.14. Найдите  в группе
в группе  , если
, если 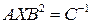 , где
, где
 ,
,  ,
,
 .
.
6.15. Найдите  в группе
в группе  , если
, если  , где
, где
 ,
,  ,
,  .
.
6.16. Докажите, что в группе  все элементы имеют конечный порядок.
все элементы имеют конечный порядок.
6.17. Докажите, что множество всех целочисленных ортогональных матриц порядка 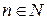 образует группу относительно умножения и найдите порядок этой группы.
образует группу относительно умножения и найдите порядок этой группы.
6.18. Докажите, что если в группе все элементы имеют порядок 2, то группа является абелевой.
6.19. Найдите все гомоморфизмы из группы  в группу
в группу  , а также ядра и образы этих гомоморфизмов.
, а также ядра и образы этих гомоморфизмов.
6.20. Найдите число гомоморфизмов, действующих из группы  в группу
в группу  , если:
, если:
1)  ,
,  ;
;
2)  ,
,  ;
;
3)  ,
,  .
.
6.21. Найдите все образующие элементы группы  , если:
, если:
1)  ;
;
2)  , где
, где 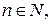
 .
.
Кольца.
Непустое множество К называется кольцом, если на нем определены две алгебраические операции (назовем их сложение и умножение), удовлетворяющие следующим условиям:
1) (К, +) – абелева группа;
2) умножение ассоциативно;
3) сложение и умножение связаны законами дистрибутивности, т.е. 
 для любых
для любых 
Обозначим через 0 нейтральный элемент кольца К относительно сложения.
Кольцо называется коммутативным, если умножение в нем коммутативно. Кольцо называется кольцом с единицей, если в нем существует нейтральный элемент 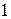 относительно умножения. Кольцо называется кольцом без делителей нуля, если
относительно умножения. Кольцо называется кольцом без делителей нуля, если  для любых ненулевых элементов
для любых ненулевых элементов  кольца. Коммутативное кольцо с единицей без делителей нуля называется областью целостности.
кольца. Коммутативное кольцо с единицей без делителей нуля называется областью целостности.
В кольце К с единицей множество К * всех обратимых элементов является группой относительно умножения. Группа К * называется мультипликативной группой кольца К.
Пусть  - кольца. Отображение
- кольца. Отображение  называется гомоморфизмом кольца
называется гомоморфизмом кольца 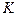 в кольцо
в кольцо  если
если  φ (g 1+ g 2)= = φ (g 1)+ φ (g 2) для любых
φ (g 1+ g 2)= = φ (g 1)+ φ (g 2) для любых  Биективный гомоморфизм колец называется изоморфизмом колец. Обозначение:
Биективный гомоморфизм колец называется изоморфизмом колец. Обозначение: 
Пусть  - непустое подмножество множества
- непустое подмножество множества 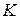 ; если
; если  является кольцом, то кольцо
является кольцом, то кольцо  называется подкольцом кольца
называется подкольцом кольца 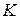 и обозначается
и обозначается  . Подкольцо I кольца К называется идеалом кольца К, если
. Подкольцо I кольца К называется идеалом кольца К, если 
 и обозначается
и обозначается  . Пусть
. Пусть 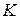 - коммутативное кольцо с единицей,
- коммутативное кольцо с единицей,  - непустое подмножество кольца
- непустое подмножество кольца 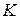 , тогда множество
, тогда множество  является идеалом кольца
является идеалом кольца 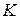 и называется идеалом, порождённым множеством
и называется идеалом, порождённым множеством  ; обозначение:
; обозначение:  . Идеал, порождённый одним элементом кольца
. Идеал, порождённый одним элементом кольца 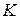 называется главным идеалом.
называется главным идеалом.
Непустое подмножество I кольца К является в К идеалом тогда и только тогда, когда выполняются следующие условия:  для любых
для любых 
 для любых
для любых 
Идеал I кольца K является нормальной подгруппой аддитивной группы кольца К.
На множестве смежных классов фактор-группы K / I определим операцию умножения смежных классов следующим образом:  Множество всех смежных классов кольца К по идеалу I относительно сложения и умножения классов является кольцом. Это кольцо называется фактор-кольцом кольца К по идеалу I и обозначается, как и фактор-группа, K / I.
Множество всех смежных классов кольца К по идеалу I относительно сложения и умножения классов является кольцом. Это кольцо называется фактор-кольцом кольца К по идеалу I и обозначается, как и фактор-группа, K / I.
Пусть  кольца,
кольца,  – гомоморфизм колец,
– гомоморфизм колец,  нуль кольца
нуль кольца  Ядром гомоморфизма
Ядром гомоморфизма  называется множество Ker φ = ={ a Î K: φ (a)=0’}. Ядро произвольного гомоморфизма
называется множество Ker φ = ={ a Î K: φ (a)=0’}. Ядро произвольного гомоморфизма  является идеалом кольца К.
является идеалом кольца К.
Пусть  - гомоморфизм колец, тогда
- гомоморфизм колец, тогда 
Важным примером кольца является следующее кольцо.
Пусть m – фиксированное натуральное число. Множество  является идеалом в кольце целых чисел Z. Фактор-кольцо кольца Z по идеалу
является идеалом в кольце целых чисел Z. Фактор-кольцо кольца Z по идеалу  называется кольцом вычетов по модулю m и обозначается
называется кольцом вычетов по модулю m и обозначается 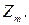
Пусть 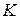 - область целостности; функция
- область целостности; функция  называется нормой в
называется нормой в 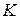 , если:
, если:
1) 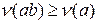 для любых
для любых 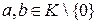 ;
;
2) для любых 
 существуют
существуют  , такие, что
, такие, что  и либо
и либо 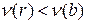 , либо
, либо  .
.
Область целостности 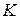 , на которой можно задать норму
, на которой можно задать норму  , называется евклидовым кольцом. Пусть
, называется евклидовым кольцом. Пусть 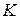 - евклидово кольцо. Элемент
- евклидово кольцо. Элемент  называется делителем элемента
называется делителем элемента 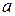 , если существует
, если существует  , такое, что
, такое, что  . Пусть
. Пусть  - ненулевые элементы евклидова кольца
- ненулевые элементы евклидова кольца 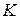 , элемент
, элемент  называется наибольшим общим делителем элементов
называется наибольшим общим делителем элементов 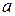 и
и  , если
, если 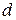 является делителем элементов
является делителем элементов 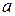 ,
,  и для любого общего делителя
и для любого общего делителя 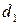 элементов
элементов 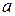 ,
,  выполняется условие
выполняется условие  (обозначение наибольшего общего делителя:
(обозначение наибольшего общего делителя:  ). Наибольший общий делитель
). Наибольший общий делитель  определён однозначно с точностью до умножения на обратимый элемент кольца
определён однозначно с точностью до умножения на обратимый элемент кольца 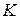 . В евклидовом кольце
. В евклидовом кольце 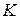 для нахождения наибольшего общего делителя чисел
для нахождения наибольшего общего делителя чисел 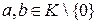 ,
,  , используют алгоритм Евклида: элемент а разделим на b с остатком:
, используют алгоритм Евклида: элемент а разделим на b с остатком:  где
где  или
или  . Если
. Если  то
то  Если
Если  то разделим b на
то разделим b на  с остатком:
с остатком: 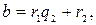 где
где  или
или  . Если
. Если  то
то  Если
Если  то разделим
то разделим  на
на  с остатком:
с остатком:  где
где  или
или  . И так далее продолжаем эту процедуру. Последний ненулевой остаток и будет наибольшим общим делителем элементов a и b.
. И так далее продолжаем эту процедуру. Последний ненулевой остаток и будет наибольшим общим делителем элементов a и b.
Пример 1. Образует ли кольцо множество рациональных чисел, в несократимой записи которых знаменатели не делятся на фиксированное простое число 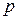 ?
?
Решение. Обозначим через  множество
множество
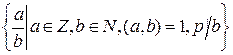 .
.
Пусть  , тогда
, тогда  , где
, где 
 ,
,  . Очевидно,
. Очевидно,  . Так как
. Так как 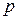 не делит число
не делит число  , то
, то 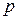 не делит
не делит  . Следовательно,
. Следовательно,  . Далее
. Далее  , где
, где 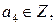
 ,
, 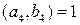 . Так как
. Так как  , то
, то 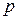 не делит
не делит  . Отсюда
. Отсюда 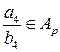 . Множество
. Множество  образует абелеву группу относительно сложения:
образует абелеву группу относительно сложения:  - нейтральный элемент, обратным элементом к
- нейтральный элемент, обратным элементом к 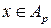 является противоположное число
является противоположное число  , сложение ассоциативно и коммутативно. Умножение коммутативно. Кроме того,
, сложение ассоциативно и коммутативно. Умножение коммутативно. Кроме того, 
 для любых
для любых 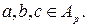 Поэтому
Поэтому  - кольцо.
- кольцо.
Дата публикования: 2015-11-01; Прочитано: 1016 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
