Обратная матрица

Для каждого числа а¹0 существует обратное число а^-1 такое, что произведение а×а^-1=1. Для квадратных матриц вводится аналогичное понятие.

Определение. Если существуют квадратные матрицы Х и А одного порядка, удовлетворяющие условию:

XA = AX = E,

где Е - единичная матрица того же самого порядка, что и матрица А, то матрица Х называется обратной к матрице А и обозначается А^-1.

Из определения следует, что только квадратная матрица имеет обратную; в этом случае и обратная матрица является квадратной того же порядка.

Однако, не каждая квадратная матрица имеет обратную. Если условие а¹0 является необходимым и достаточным для существования числа а^-1, то для существования матрицы А^-1 таким условием является требование DA ¹0.

Определение. Квадратная матрица n -го порядка называется невырожденной (неособенной), если ее определитель DA ¹0.

Если же DA= 0, то матрица А называется вырожденной (особенной).

Теорема (необходимое и достаточное условие существования обратной матрицы). Если квадратная матрица неособенная (т.е. ее определитель не равен нулю), то для нее существует единственная обратная матрица.

Доказательство.

I. Необходимость. Пусть матрица А имеет обратную А^-1, т.е. АА^-1= А^-1А=Е. По свойству 3 определителей (§ 11) имеем D(АА^-1)= D(А^-1) D(А)= D(Е)=1, т.е. DA ¹0 и DA^-1 ¹0.

I I. Достаточность. Пусть квадратная матрица А неособенная, т.е. DA ¹0. Напишем транспонированную матрицу А^Т:

А^Т = .

В этой матрице каждый элемент заменим его алгебраическим дополнением, получим матрицу:

А^* = .

Матрица А^* называется присоединенной матрицей к матрице А.

Найдем произведение АА^* (и А^*А):

АА^* = ,

Где диагональные элементы = DA,

=DA,

:

:

=DA.(формуле 11.1 §11)

А все остальные недиагональные элементы матрицы АА^* равны нулю по свойству 10 §11, например:

,

и т.д. Следовательно,

АА^* = или АА^* = DA = DA×Е.

Аналогично доказывается, что А^*А = DA×Е.

Разделив оба полученных равенства на DA, получим: 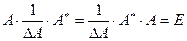. Отсюда, по определению обратной матрицы, следует существование обратной матрицы

, т.к. АА^-1=А^-1А=Е.

Существование обратной матрицы доказано. Докажем единственность. Предположим, что существует еще другая обратная матрица F для матрицы А, тогда AF = E и FA = E. Умножив обе части первого равенства на А^-1 слева, а второго на А^-1 справа, получим: А^-1AF = А^-1E и FA А^-1 = E А^-1, откуда EF = А^-1E и FE = E А^-1. Следовательно, F = А^-1. Единственность доказана.

Пример. Дана матрица А = , найти А^-1.

Алгоритм вычисления обратной матрицы:

1. Находим определитель исходной матрицы. Если DA =0, то матрица А-вырожденная и обратная матрица А^-1 не существует. Если DA ¹0, то матрица А-невырожденная и обратная матрица А^-1 существует.
2. Находим алгебраические дополнения элементов исходной матрицы А_ij и составляем из них присоединенную матрицу А^*, записывая алгебраические дополнения элементов строки в столбец.
3. Вычисляем обратную матрицу по формуле: .
4. Проверить правильность вычисления обратной матрицы

Свойства обратных матриц.

1) (A^-1)^-1 = A;

2) (AB)^-1 = B^-1A^-1

3) (A^T)^-1 = (A^-1)^T.