Линейные операции над векторами в координатной форме

1. При умножении вектора на число все его координаты умножаются на это число, т.е. если .

Действительно, используя свойства операций умножения вектора на число и сложении векторов будем иметь

.

При сложении векторов их соответствующие координаты складываются, т.е. если .

Доказательство очевидно.

Условие коллинеарности двух векторов в коорднинатной форме.

Два вектора коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны. Т.е. если , то .

Доказательство:

1. Пусть вектор коллинеарен , тогда найдется λ такое, что 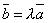. Значит, и . Поскольку разложение вектора по элементам базиса 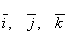единственно, то .

2. Пусть выполняется равенство . Обозначим коэффициент пропорциональности через λ. Тогда и, следовательно, , т.е. . Теорема доказана.

Пример.

1. Даны векторы . Найти вектор .

.

2. Найти координаты вектора в базисе, образованном векторами , , .

Обозначим координаты вектора в новом базисе . Тогда в новом базисе будем иметь:

Итак, .

Рассмотрим две произвольные функцию y= x³. Будем рассматривать равенство y = x³ как уравнение относительно x. Это уравнение для каждого значения у определяет единственное значение x: . Геометрически это значит, что всякая прямая параллельная оси Ox пересекает график функции y= x³ только в одной точке. Поэтому мы можем рассматривать x как функцию от y. Функция называется обратной по отношению к функции y= x³.

Прежде чем перейти к общему случаю, введем определения.

Функция y = f(x) называется возрастающей на некотором отрезке, если большему значению аргумента x из этого отрезка соответствует большее значение функции, т.е. если x ₂> x ₁, вектора .

Очевидно, что . Но по определению координат вектора и . Следовательно,

Таким образом, чтобы найти координаты вектора , нужно из координат его конца вычесть соответствующие координаты начала.

Примеры.

3. Заданы точки A (1; -2; 3), B (2; 0; -1). Найти вектор .

4. Даны A (-2; 3; 1), В (-1; 2; 0), С (0; 1; 1). Найти .

5. Известно, что . Найти координаты точки D, если

А (3; -4; -1), В (-4; 4; 1), С (-3; -5; 4).

Пусть тогда

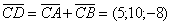. С другой стороны . Следовательно, должно выполняться равенство (x +3; y +5; z -4)=(5;10;-8). Отсюда

x =2, y =5, z =-4, т.е. точка D имеет координаты D (2; 5; -4).