 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Скалярное произведение векторов и его свойства
|
|
 Мы рассмотрели умножение вектора на число. Однако во многих задачах механики и физики встречается операция умножения вектора на вектор. Но при этом результат может быть как числом, так и вектором. Поэтому рассматривают два вида умножения векторов: скалярное и векторное.
Мы рассмотрели умножение вектора на число. Однако во многих задачах механики и физики встречается операция умножения вектора на вектор. Но при этом результат может быть как числом, так и вектором. Поэтому рассматривают два вида умножения векторов: скалярное и векторное.
Пусть даны два вектора  и
и  , угол между, которыми равен
, угол между, которыми равен  .
.
Скалярным произведением векторов  и
и  называется число, равное произведению длин этих векторов на косинус угла между ними. Скалярное произведение обозначается
называется число, равное произведению длин этих векторов на косинус угла между ними. Скалярное произведение обозначается  . Итак,
. Итак, 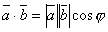 .
.
Если один из векторов нулевой, то угол не определен, и скалярное произведение по определения считается равным нулю.
Рассмотрим свойства скалярного произведения.
- Скалярное произведение двух векторов подчиняется коммутативному закону, т.е. для любых векторов
 и
и 
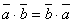 .
.
Очевидно, из определения скалярного произведения:
 .
.
- Для любого числа λ и любых векторов
 имеем:
имеем:
 .
.
Доказательство. Ограничимся случаем, когда λ > 0. В этом случае угол между векторами  и
и  совпадает с углом между векторами
совпадает с углом между векторами  и
и  ,
,  .
.
Поэтому  . Откуда
. Откуда 
Аналогично доказывается и равенство  .
.
Случай λ <0 рассмотреть самостоятельно.
- Для любых векторов
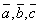 выполняется равенство
выполняется равенство  .
.
Доказательство. Используя определение скалярного произведения и свойства проекций вектора на ось, будем иметь

- Для любого вектора
 выполняется соотношение
выполняется соотношение  .
.
Действительно, так как  , то
, то  .
.
Из этого свойства в частности следует  .
.
- Скалярное произведение двух векторов равно нулю тогда и только тогда,когда равен нулю один из сомножителей или векторы перпендикулярны.
Это свойство очевидно из определения скалярного произведения.
Таким образом, необходимым и достаточным условием ортогональности двух векторов является равенство нулю их скалярного произведения.
Пример. Дан вектор  . Известно, что
. Известно, что 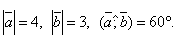
Найти 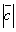 .
.
Имеем  , т.е.
, т.е.  .
.
Найдем: 
Следовательно,  .
.
 Рассмотрим, как находится скалярное произведение векторов, если они заданы в координатной форме. Пусть даны два вектора
Рассмотрим, как находится скалярное произведение векторов, если они заданы в координатной форме. Пусть даны два вектора  и
и  .
.
Рассмотрим сначала все возможные скалярные произведения векторов  друг на друга.
друг на друга.
Поэтому

Итак, скалярное произведение векторов равно сумме произведений соответствующих координат:  .
.
Это соотношение позволяет вычислить длину вектора через его координаты:
 .
.
Далее из определения скалярного произведения  находим
находим
 .
.
Выражая скалярное произведение и длины векторов через их координаты,получим формулу для нахождения косинуса угла между векторами
 .
.
Условие ортогональности двух векторов:
 или
или  .
.
Т.о., для того чтобы два вектора были перпендикулярны необходимо и достаточно, чтобы сумма произведений соответствующих координат этих векторов была равна нулю.
Примеры.
- Пусть А (-1; 1; 0), B (3; 1; -2),
 . Найти:
. Найти: -
 ;
; -
 и
и 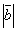 ;
; -
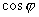 .
. -
 .
. -
 .
. -
 .
. - Найти
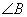 в
в  , если известны координаты его вершин A (1; 5; 6),
, если известны координаты его вершин A (1; 5; 6),
 B (5; 3; 10), C (2; 1; 14).
B (5; 3; 10), C (2; 1; 14).

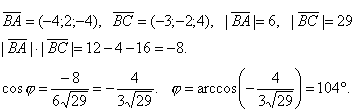
- При каком значении m векторы
 и
и  перпендикулярны?
перпендикулярны?
Условие ортогональности двух векторов  .
.
 . Следовательно, m = 15.
. Следовательно, m = 15.
Дата публикования: 2015-11-01; Прочитано: 771 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
