 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Линейные операции над векторами
|
|
1. Умножение вектора на число.
Произведением вектора  на число λ называется новый вектор
на число λ называется новый вектор  такой, что:
такой, что:
1.  ;
;
2. вектор  коллинеарен вектору
коллинеарен вектору  ;
;
3. векторы  и
и  направлены одинаково, если λ>0 и противоположно, если λ< 0. (Если λ=0, то из условия 1 следует, что
направлены одинаково, если λ>0 и противоположно, если λ< 0. (Если λ=0, то из условия 1 следует, что 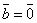 ).
).
Произведение вектора  на число λ обозначается
на число λ обозначается  .
.

Например,  есть вектор, направленный в ту же сторону, что и вектор
есть вектор, направленный в ту же сторону, что и вектор  , и имеющий длину, вдвое меньшую, чем вектор
, и имеющий длину, вдвое меньшую, чем вектор  .
.
Введённая операция обладает следующими свойствами:
4. Для любых чисел a и b и вектора  выполняется равенство
выполняется равенство  .
.
Действительно, векторы, стоящие в обеих частях равенства имеют одинаковую длину  . Кроме того, ясно, что они одинаково направлены, т.к. их направление совпадает с направлением вектором
. Кроме того, ясно, что они одинаково направлены, т.к. их направление совпадает с направлением вектором  , если a и b одного знака, и противоположно направлению
, если a и b одного знака, и противоположно направлению  , если a и b разных знаков.
, если a и b разных знаков.
5. Пусть дан вектор  . Для любого коллинеарного ему вектора
. Для любого коллинеарного ему вектора  найдётся и притом только одно число l, удовлетворяющее равенству
найдётся и притом только одно число l, удовлетворяющее равенству  .
.
Доказательство свойства 2:
1. Пусть  . Рассмотрим вектор
. Рассмотрим вектор  . Очевидно,
. Очевидно,  . Кроме того
. Кроме того  , поэтому
, поэтому  . Из этих двух свойств следует, что
. Из этих двух свойств следует, что  , а значит
, а значит  .
.
2. Аналогично, если  . Тогда
. Тогда  .
.
Единственность числа λ следует из того, что при умножении вектора  на два разных числа, получаем два разных вектора.
на два разных числа, получаем два разных вектора.
2. Сложение векторов.
Пусть  и и  – два произвольных вектора. Возьмём произвольную точку O и построим вектор – два произвольных вектора. Возьмём произвольную точку O и построим вектор  . После этого из точки A отложим вектор . После этого из точки A отложим вектор  . Вектор . Вектор 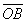 , соединяющий начало первого вектора , соединяющий начало первого вектора  c концом второго c концом второго  , называется суммой этих векторов и обозначается , называется суммой этих векторов и обозначается  .
Сформулированное определение сложения векторов называют правилом параллелограмма, так как ту же самую сумму векторов можно получить следующим образом. Отложим от точки O векторы .
Сформулированное определение сложения векторов называют правилом параллелограмма, так как ту же самую сумму векторов можно получить следующим образом. Отложим от точки O векторы  и и 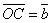 . Построим на этих векторах параллелограмм ОАВС. Так как векторы . Построим на этих векторах параллелограмм ОАВС. Так как векторы  , то вектор , то вектор 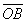 , являющийся диагональю параллелограмма, проведённой из вершины O, будет очевидно суммой векторов , являющийся диагональю параллелограмма, проведённой из вершины O, будет очевидно суммой векторов 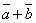 . .
|  
|
3.
4. Легко проверить следующие свойства сложения векторов.
1. Ясно, что прибавление нулевого вектора к некоторому вектору ā не меняет вектора  , т.е.
, т.е.  .
.
2. Сложение векторов коммутативно, т.е.  .
.
Это свойство сразу следует из правила параллелограмма.
3.
 Сложение векторов ассоциативно, т.е. для любых трёх векторов
Сложение векторов ассоциативно, т.е. для любых трёх векторов  . Поэтому сумму трёх векторов часто записывают просто
. Поэтому сумму трёх векторов часто записывают просто  .
.
Сумму трёх векторов можно получить следующим образом. Из произвольной точки O откладывается вектор, равный первому вектору. К его концу присоединяется начало второго, к концу второго – начало третьего. Вектор, соединяющий начало первого вектора с концом последнего, будет суммой данных векторов. Аналогично строится сумма любого конечного числа векторов.
4. Для любого числа λ и любых векторов  и
и 
 .
.
 Заметим, что при умножении векторов на число λ меняются только размеры векторов, т.е. масштаб чертежа, фигуры остаются подобными. Поэтому, так как векторы
Заметим, что при умножении векторов на число λ меняются только размеры векторов, т.е. масштаб чертежа, фигуры остаются подобными. Поэтому, так как векторы  образуют стороны и диагональ параллелограмма, то, умножив все члены на λ, т.е. изменив лишь размеры векторов одинаковым образом, мы получим снова параллелограмм, а значит, сохранится равенство
образуют стороны и диагональ параллелограмма, то, умножив все члены на λ, т.е. изменив лишь размеры векторов одинаковым образом, мы получим снова параллелограмм, а значит, сохранится равенство  .
.
5. Для любых чисел a и b и любого вектора  выполняется равенство
выполняется равенство 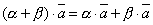 .
.
5. Разность векторов.
Вектор, коллинеарный данному вектору  , равный ему по длине и противоположно направленный, называется противоположным вектором для вектора
, равный ему по длине и противоположно направленный, называется противоположным вектором для вектора  и обозначается
и обозначается  . Противоположный вектор
. Противоположный вектор  можно рассматривать как результат умножения вектора
можно рассматривать как результат умножения вектора  на число λ = –1:
на число λ = –1:  .
.
 Разностью двух векторов
Разностью двух векторов  и
и  называется вектор
называется вектор 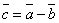 , равный сумме векторов
, равный сумме векторов  и
и  , т.е.
, т.е.  .
.
Очевидно, что  , для любого вектора
, для любого вектора  .
.
Легко показать, что  .
.
Действительно, 
Таким образом, если  .
.
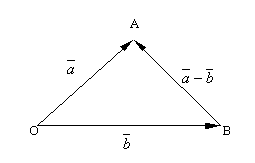
Из определения суммы двух векторов вытекает правило построения вектора разности. Откладываем векторы  и
и  из общей точки O. Чтобы найти вектор-разность, нужно к
из общей точки O. Чтобы найти вектор-разность, нужно к  добавить вектор
добавить вектор  или
или  . Тогда
. Тогда 
 . Вектор
. Вектор  , соединяющий концы векторов
, соединяющий концы векторов  и
и  и направленный от "вычитаемого" к "уменьшаемому" (т.е. от второго вектора к первому), и будет разностью
и направленный от "вычитаемого" к "уменьшаемому" (т.е. от второго вектора к первому), и будет разностью  . Действительно, по правилу сложения векторов
. Действительно, по правилу сложения векторов  или
или  .
.
Таким образом, если на векторах  и
и  , отложенных из общей точки O, построить параллелограмм OACB, то вектор
, отложенных из общей точки O, построить параллелограмм OACB, то вектор  , совпадающий с одной диагональю параллелограмма, равен сумме
, совпадающий с одной диагональю параллелограмма, равен сумме 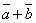 , а вектор
, а вектор  , совпадающий с другой диагональю, равен разности
, совпадающий с другой диагональю, равен разности  .
.
Проекция вектора на ось
усть в пространстве даны два вектора  и и  . Отложим от произвольной точки O векторы . Отложим от произвольной точки O векторы  и и  . Углом между векторами . Углом между векторами  и и  называется наименьший из углов называется наименьший из углов  . Обозначается . Обозначается  .
Рассмотрим ось l и отложим на ней единичный вектор .
Рассмотрим ось l и отложим на ней единичный вектор  (т.е. вектор, длина которого равна единице).
Под углом между вектором (т.е. вектор, длина которого равна единице).
Под углом между вектором  и осью l понимают угол и осью l понимают угол  между векторами между векторами  и и  .
Итак, пусть l – некоторая ось и .
Итак, пусть l – некоторая ось и 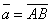 – вектор.
Обозначим через A1 и B1 проекции на ось l соответственно точек A и B. Предположим, что A1 имеет координату x1, а B1 – координату x2 на оси l.
Тогда проекцией вектора – вектор.
Обозначим через A1 и B1 проекции на ось l соответственно точек A и B. Предположим, что A1 имеет координату x1, а B1 – координату x2 на оси l.
Тогда проекцией вектора  на ось l называется разность x1 – x2 между координатами проекций конца и начала вектора на ось l называется разность x1 – x2 между координатами проекций конца и начала вектора  на эту ось.
Проекцию вектора на эту ось.
Проекцию вектора  на ось l будем обозначать на ось l будем обозначать  .
Ясно, что если угол между вектором .
Ясно, что если угол между вектором  и осью l острый, то x2 > x1, и проекция x2 – x1 > 0; если этот угол тупой, то x2 < x1 и проекция x2 – x1 < 0. Наконец, если вектор и осью l острый, то x2 > x1, и проекция x2 – x1 > 0; если этот угол тупой, то x2 < x1 и проекция x2 – x1 < 0. Наконец, если вектор  перпендикулярен оси l, то x2 = x1 и x2 – x1 = 0.
Таким образом, проекция вектора перпендикулярен оси l, то x2 = x1 и x2 – x1 = 0.
Таким образом, проекция вектора  на ось l – это длина отрезка A1B1, взятая с определённым знаком. Следовательно, проекция вектора на ось это число или скаляр.
Аналогично определяется проекция одного вектора на другой. В этом случае находятся проекции концов даного вектора на ту прямую, на которой лежит 2-ой вектор.
Рассмотрим некоторые основные свойства проекций.
1. Проеция вектора на ось l – это длина отрезка A1B1, взятая с определённым знаком. Следовательно, проекция вектора на ось это число или скаляр.
Аналогично определяется проекция одного вектора на другой. В этом случае находятся проекции концов даного вектора на ту прямую, на которой лежит 2-ой вектор.
Рассмотрим некоторые основные свойства проекций.
1. Проеция вектора  на ось l равна произведению модуля вектора на ось l равна произведению модуля вектора  на косинус угла между вектором и осью: на косинус угла между вектором и осью:
 Доказательство. Ясно, что проекция вектора не изменится при его параллельном переносе, поэтому достаточно рассмотреть случай, когда начало вектора совпадает с началом отсчёта O оси l. Так как координата проекции начала равна нулю, то обозначим
Доказательство. Ясно, что проекция вектора не изменится при его параллельном переносе, поэтому достаточно рассмотреть случай, когда начало вектора совпадает с началом отсчёта O оси l. Так как координата проекции начала равна нулю, то обозначим  .
1. Если угол φ острый, то из прямоугольного .
1. Если угол φ острый, то из прямоугольного  получаем получаем  . Откуда . Откуда  или или  2. Если угол φ тупой, то x < 0,
2. Если угол φ тупой, то x < 0,  . Тогда из . Тогда из   или или  . Т.е. . Т.е.  .
2. Проекция суммы двух векторов на ось равна сумме проекций векторов на ту же ось: .
2. Проекция суммы двух векторов на ось равна сумме проекций векторов на ту же ось:  .
Доказательство. Пусть .
Доказательство. Пусть  . Обозначим через x1, x2 и x3 координаты проекций A1, B1, C1 на ось l точек A, B и C. Тогда . Обозначим через x1, x2 и x3 координаты проекций A1, B1, C1 на ось l точек A, B и C. Тогда  . Но . Но  .
Это свойство можно обобщить на случай любого числа слагаемых.
3. Если вектор .
Это свойство можно обобщить на случай любого числа слагаемых.
3. Если вектор  умножается на число λ, то его проекция на ось также умножается на это число: умножается на число λ, то его проекция на ось также умножается на это число:
  .
Доказательство. Пусть угол между вектором .
Доказательство. Пусть угол между вектором  и осью и осью  .
Если λ > 0, то вектор .
Если λ > 0, то вектор  имеет то же направление, что и имеет то же направление, что и  , и составляет с осью такой же угол , и составляет с осью такой же угол  .
При λ > 0 .
При λ > 0  .
Если же λ < 0, то .
Если же λ < 0, то  и и  имеют противоположные направления и вектор имеют противоположные направления и вектор  составляет с осью угол π – φ и составляет с осью угол π – φ и  .
Следствие. Проекция разности двух векторов на ось равна разности проекций этих векторов на ту же ось. .
Следствие. Проекция разности двух векторов на ось равна разности проекций этих векторов на ту же ось.
|       
|
Дата публикования: 2015-11-01; Прочитано: 599 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
