Собственные векторы и собственные значения матрицы

Пусть задана квадратная матрица , X – некоторая матрица–столбец, высота которой совпадает с порядком матрицы A. .

Во многих задачах приходится рассматривать уравнение относительно X

,

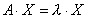где λ – некоторое число. Понятно, что при любом λ это уравнение имеет нулевое решение .

Число λ, при котором это уравнение имеет ненулевые решения, называется собственным значением матрицы A, а X при таком λ называется собственным вектором матрицы A.

Найдём собственный вектор матрицы A. Поскольку E ∙ X = X, то матричное уравнение можно переписать в виде или . В развёрнутом виде это уравнение можно переписать в виде системы линейных уравнений. Действительно .

И, следовательно,

Итак, получили систему однородных линейных уравнений для определения координат x₁, x₂, x₃ вектора X. Чтобы система имела ненулевые решения необходимо и достаточно, чтобы определитель системы был равен нулю, т.е.

Это уравнение 3-ей степени относительно λ. Оно называется характеристическим уравнением матрицы A и служит для определения собственных значений λ.

Каждому собственному значению λ соответствует собственный вектор X, координаты которого определяются из системы при соответствующем значении λ.

Примеры.

1. Найти собственные векторы и соответствующие им собственные значения матрицы .

Составим характеристическое уравнение и найдём собственные значения

1. При λ₁ = –1 получаем систему уравнений

Если x₁ = t, то , где tÎR.

2. Если λ₂ = 5

2.