Смешанное произведение трех векторов и его свойства

Смешанным произведением трёх векторов называют число, равное . Обозначается . Здесь первые два вектора умножаются векторно и затем полученный вектор 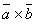умножается скалярно на третий вектор 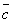. Очевидно, такое произведение есть некоторое число.

Рассмотрим свойства смешанного произведения.

1. Геометрический смысл смешанного произведения. Смешанное произведение 3-х векторов с точностью до знака равно объёму параллелепипеда, построенного на этих векторах, как на рёбрах, т.е. .

Таким образом, и .

Доказательство. Отложим векторы от общего начала и построим на них параллелепипед. Обозначим и заметим, что . По определению скалярного произведения

. Предполагая, что и обозначив через h высоту параллелепипеда, находим .

Таким образом, при

Если же , то и 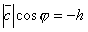. Следовательно, .

Объединяя оба эти случая, получаем или .

Из доказательства этого свойства в частности следует, что если тройка векторов правая, то смешанное произведение , а если – левая, то .

1. Для любых векторов , , 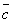справедливо равенство

.

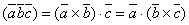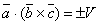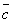Доказательство этого свойства следует из свойства 1. Действительно, легко показать, что и . Причём знаки "+" и "–" берутся одновременно, т.к. углы между векторами и и и одновременно острые или тупые.

1. При перестановке любых двух сомножителей смешанное произведение меняет знак.

Действительно, если рассмотрим смешанное произведение , то, например, или

.

1. Смешанное произведение 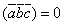тогда и только тогда, когда один из сомножителей равен нулю или векторы – компланарны.

Доказательство.

1. Предположим, что 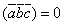, т.е. 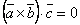, тогда или или .

Если , то или или 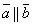. Поэтому – компланарны.

Если , то , , 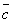- компланарны.

1. Пусть векторы – компланарны и α – плоскость, которой они параллельны, т. е. 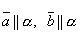и . Тогда , а значит , поэтому или .

Т.о., необходимым и достаточным условием компланарности 3-х векторов является равенство нулю их смешанного произведения. Кроме того, отсюда следует, что три вектора образуют базис в пространстве, если .

Если векторы заданы в координатной форме , то можно показать, что их смешанное произведение находится по формуле:

.

Т. о., смешанное произведение равно определителю третьего порядка, у которого в первой строке стоят координаты первого вектора, во второй строке – координаты второго вектора и в третьей строке – третьего вектора.

Примеры.

1. Показать, что векторы образуют базис в пространстве.

, т.е. векторы – базис.

1. Найти объём пирамиды с вершинами в точках A (2; -2; 0), B (-1; 4; -4), C (4; -8; 5), D (1; -7; 0). Правую или левую тройку образуют векторы и ?

Т. к. , то тройка векторов левая.