 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Свойства скалярного произведения
|
|
1) Коммутативность: 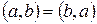 .
.
Действительно, 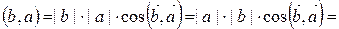 (т.к.
(т.к. 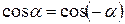 , т.е. четная функция, то
, т.е. четная функция, то  )
) 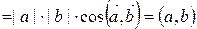 .
.
2) Скалярное произведение двух векторов равно длине одного вектора умноженной на проекцию другого на направление первого.
Действительно, 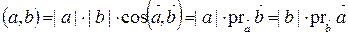 .
.
Отсюда видно, что если  , то
, то 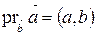 .
.
Следовательно, проекция вектора на ось равна скалярному произведению этого вектора на направляющий вектор оси.
3) 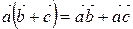 .
.
Действительно, 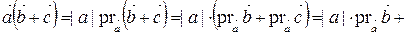
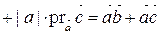 .
.
4) 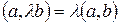 .
.
Действительно,  .
.
5) Для того, что бы два ненулевых вектора были перпендикулярны, необходимо и достаточно, чтобы их скалярное произведение было равно нулю.
 Пусть
Пусть 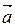 ^
^ 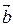 Þ
Þ 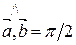 Þ
Þ 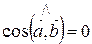 Þ
Þ 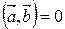 .
.
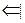 Пусть
Пусть 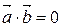 Þ
Þ 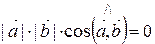 , т.к.
, т.к.  ,
, 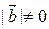 Þ
Þ 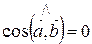 Þ
Þ 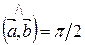 Þ
Þ 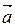 ^
^ 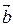 .
.
6) Пусть 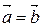 Þ
Þ  , т.е.
, т.е. 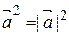 Þ скалярный квадрат вектора
Þ скалярный квадрат вектора 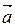 равен квадрату длины вектора Þ
равен квадрату длины вектора Þ 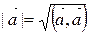 .
.
Тогда 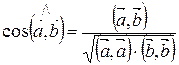
Вычисление скалярного произведения в прямоугольных координатах.
Пусть  ,
, 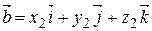 .
.
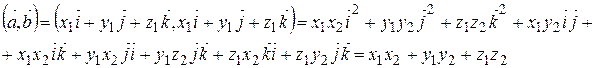
(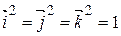 ,
, 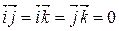 ).
).
В прямоугольной декартовой системе координат скалярное произведение векторов равно сумме произведений соответствующих координат.
Некоторые метрические формулы.
1) 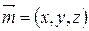 Þ
Þ 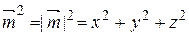 Þ
Þ 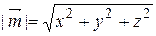
2) 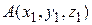 ,
,  Þ
Þ 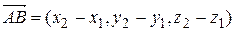 Þ
Þ 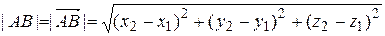 .
.
3) Если 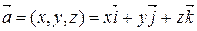 , то
, то 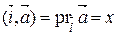 ,
, 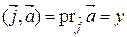 ,
, 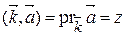 .
.
Т.о., прямоугольные координаты вектора есть его ортогональные проекции на оси прямоугольной системы координат.
4) Пусть 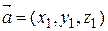 ,
, 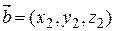 Þ
Þ 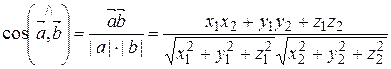 .
.
Таким образом, 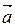 ^
^ 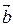 Û
Û  .
.
Из формулы косинуса угла между векторами легко найти углы a, b, g, которые вектор 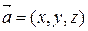 образует с осями координат. Эти углы называются направляющими углами.
образует с осями координат. Эти углы называются направляющими углами.
Имеем:
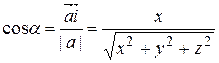 ,
, 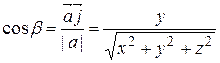 ,
, 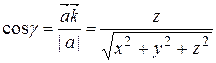 .
.
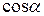 ,
, 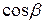 ,
, 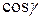 называются направляющими косинусами вектора
называются направляющими косинусами вектора 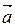 . Они связаны соотношением
. Они связаны соотношением
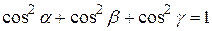 .
.
Следовательно, вектор 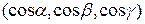 есть координаты вектора
есть координаты вектора 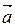 , т.е. вектора
, т.е. вектора 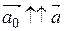 и
и 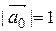 .
.
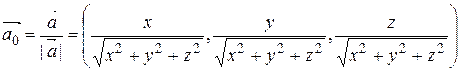 .
.
5о. Векторное произведение векторов
Пусть даны два неколлинеарных и не нулевых вектора 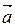 и
и 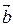 .
.
Определение 1. Векторным произведением векторов 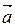 и
и 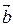 называется вектор
называется вектор 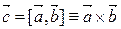 , удовлетворяющий свойствам:
, удовлетворяющий свойствам:
1. 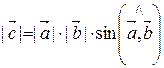 .
.
2. 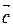 ^
^ 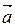 и
и 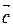 ^
^ 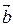 .
.
3. тройка векторов 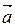 ,
, 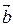 ,
, 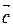 – правая.
– правая.
Если один из векторов нулевой, или вектора коллинеарны, то их векторное произведение равно нулю.
Дата публикования: 2015-11-01; Прочитано: 316 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
