Группа IV. Аксиомы непрерывности

IV₁ (аксиома Архимеда). Пусть АВ и CD - какие-нибудь отрез­ки. Тогда на прямой АВ существует конечное множество точек , таких, что выполняются условия:

а) А—А;

б) ;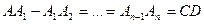

в)

IV₂ (аксиома Кантора). Пусть на произвольной прямой а дана бесконечная последовательность отрезков , из которых каждый последующий лежит внутри предыдущего и, кроме того, для любого отрезка CD найдется натуральное число n, такое, что . Тогда на прямой а существует точка М, принадлежащая каждому из отрезков данной последовательности.

Ясно, что такая точка М единственная. В самом деле, если пред­положить, что точка N, отличная от точки М, также принадлежит каждому из отрезков данной последовательности, то получим при любом n, что противоречит аксиоме.

К важнейшим следствиям из аксиом групп I—IV относится теория измерения отрезков и углов[5]. Построив теорию измерения отрезков, легко дока­зать, что существует биекция множества точек прямой на множество R вещественных чисел, сохраняющая порядок. Таким образом, точки на прямой расположены непрерывно одна за другой, как и числа во множестве R. Следствиями аксиом групп I - IV являются также известные теоремы о пересечении прямой и окружности и двух окруж­ностей.

6.3. Для обоснования евклидовой теории параллельных Гильберт к аксиомам групп I - IV добавляет еще одну аксиому параллельных прямых.

Группа V. Аксиома параллельности.

Пусть а — произвольная прямая, а А — точка, не лежащая на этой прямой. Тогда в плоскости, определяемой точкой А и прямой а, существует не более одной прямой, проходящей через А и не пере­секающей а.

Ранее было доказано, что эта аксиома эквивалентна V постулату Евклида.

На основе всех аксиом групп I - V можно построить теорию па­раллельных прямых по Евклиду, доказать теоремы о сумме углов треугольника и выпуклого многоугольника, изучить свойства парал­лелограммов и трапеций, построить теорию подобия и т. д. Заметим еще, что аксиомы групп I - V позволяют обосновать обычную триго­нометрию, изучаемую в средней школе, а также декартову анали­тическую геометрию. В частности, пользуясь теоремой Пифагора, для доказательства которой необходимо использовать аксиому V, вы­водится известная формула для вычисления расстояния между двумя точками по координатам этих точек. Кроме того, доказывается, что плоскость в пространстве определяется уравнением первой сте­пени, а прямая — системой двух уравнений с тремя переменными. Таким образом, мы получаем возможность приложить алгебру к до­казательству теорем геометрии.

Отметим, наконец, что, пользуясь аксиомам групп I - V, мож­но ввести понятия площади многоугольника и объема многогран­ника.

Замечания.

1. В «Основаниях геометрии» Гильберта груп­пу IV аксиом составляет аксиома параллельности, а группу V — аксиомы непрерывности, причем вместо аксиомы Кантора Гильберт берет другую аксиому, которую он назвал аксиомой линейной полно­ты. Формулировка этой аксиомы довольно громоздкая, и мы ее не при­водим.

2. Геометрию, построенную на аксиомах групп I—IV, называют абсолютной геометрией. Все теоремы и определения, сформулиро­ванные нами в §5 и п. 1,2 §6 являются теоремами абсолютной геометрии. К ним еще следует присоединить лемму 1 §3 и теоре­му 4 того же параграфа, которые доказываются без помощи аксиомы параллельности.