Смешанное произведение векторов. Свойства смешанного произведения. Геометрический смысл

Выясним геометрический смысл смешанного произведения векторов 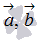и .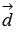

Отложим векторы 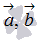и 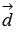от одной точки и построим параллелепипед на этих векторах как на сторонах.

Обозначим 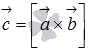. В этом случае смешанное произведение можно записать как 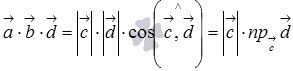, где 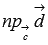- числовая проекция вектора 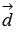на направление вектора .

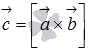Абсолютная величина числовой проекции 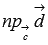равна высоте параллелепипеда, построенного на векторах 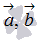и 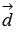, так как вектор 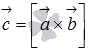перпендикулярен и вектору 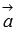и вектору 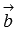по определению векторного произведения. А в разделе геометрический смысл векторного произведения мы выяснили, что величина 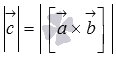представляет собой площадь параллелограмма, построенного на векторах 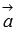и 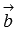. Таким образом, модуль смешанного произведения 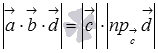- это произведение площади основания на высоту параллелепипеда, построенного на векторах 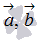и .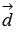

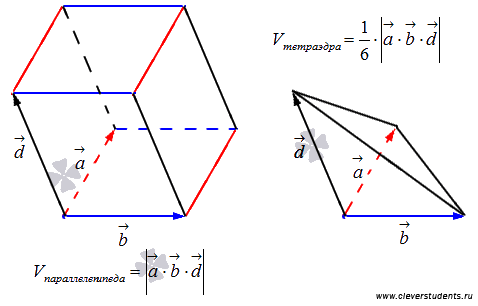
Следовательно, абсолютная величина смешанного произведения векторов представляет собой объем параллелепипеда: . В этом заключается геометрический смысл смешанного произведения векторов.

Объем тетраэдра, построенного на векторах 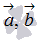и 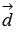, равен одной шестой объема соответствующего параллелепипеда, таким образом, .