 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Ортогональные векторы. Ортонормированный базис
|
|
Определение. Два вектора называются ортогональными, если угол междуними равен прямому углу, т.е. 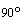 .
.
Обозначение:  – векторы
– векторы 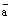 и
и 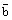 ортогональны.
ортогональны.
Определение. Тройка векторов 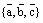 называется ортогональной, если эти векторы попарно ортогональны друг другу, т.е.
называется ортогональной, если эти векторы попарно ортогональны друг другу, т.е. 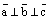 ,
, 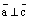 .
.
Определение. Тройка векторов 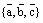 называется ортонормированной, если она ортогональная и длины всех векторов равны единице:
называется ортонормированной, если она ортогональная и длины всех векторов равны единице: 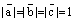 .
.
Замечание. Из определения следует, что ортогональная и, следовательно, ортонормированная тройка векторов является некомпланарной.
Определение. Упорядоченная некомпланарная тройка векторов 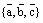 , отложенных от одной точки, называется правой (правоориентированной), если при наблюдении с конца третьего вектора
, отложенных от одной точки, называется правой (правоориентированной), если при наблюдении с конца третьего вектора 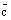 на плоскость, в которой лежат первые два вектора
на плоскость, в которой лежат первые два вектора 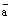 и
и 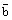 , кратчайший поворот первого вектора
, кратчайший поворот первого вектора 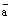 ко второму
ко второму 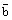 происходит против часовой стрелки. В противном случае тройка векторов называется левой (левоориентированной).
происходит против часовой стрелки. В противном случае тройка векторов называется левой (левоориентированной).
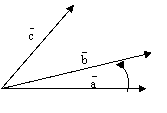
рис.6.
Здесь, на рис.6 изображена правая тройка векторов 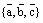 . На следующем рис.7 изображена левая тройка векторов
. На следующем рис.7 изображена левая тройка векторов 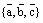 :
:

рис.7.
Определение. Базис 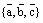 векторного пространства
векторного пространства 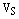 называется ортонормированным, если
называется ортонормированным, если 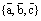 ортонормированная тройка векторов.
ортонормированная тройка векторов.
Обозначение. В дальнейшем мы будем пользоваться правым ортонормированным базисом 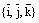 , см. следующий рисунок:
, см. следующий рисунок:
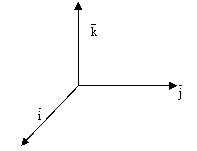
рис.9.
Любой вектор можно разложить по этому базису:
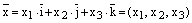 .
.
Дата публикования: 2015-10-09; Прочитано: 735 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
