Критерий для проверки гипотезы о математическом ожидании

Пусть генеральная совокупность Х имеет нормальное распределение, и требуется проверить предположение о том, что ее математическое ожидание равно некоторому числу 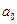. Рассмотрим две возможности.

1) Известна дисперсия 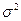генеральной совокупности. Тогда по выборке объема п найдем выборочное среднее 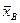и проверим нулевую гипотезу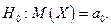

Учитывая, что выборочное среднее 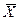является несмещенной оценкой 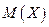, т.е. 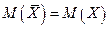, запишем нулевую гипотезу так: 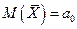. Для ее проверки выберем критерий

.

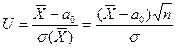Это случайная величина, имеющая нормальное распределение, причем, если нулевая гипотеза справедлива, то

Выберем критическую область в зависимости от вида конкурирующей гипотезы:

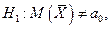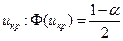- если то , критическая область двусторонняя, 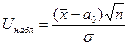, и, если 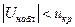, то нулевая гипотеза принимается; если |, то нулевая гипотеза отвергается.

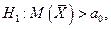- если , то 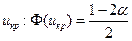, критическая область правосторонняя, и, если 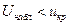, то нулевая гипотеза принимается; если 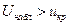, то нулевая гипотеза отвергается.

- если 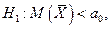, то 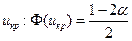, критическая область левосторонняя, и, если 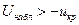, то нулевая гипотеза принимается; если 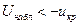, то нулевая гипотеза отвергается.

2) Дисперсия генеральной совокупности неизвестна. В этом случае выберем в качестве критерия случайную величину

,

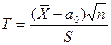где S – исправленное среднее квадратическое отклонение. Такая случайная величина имеет распределение Стьюдента с 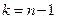степенями свободы. Рассмотрим те же, что и в предыдущем случае, конкурирующие гипотезы и соответствующие им критические области. Предварительно вычислим наблюдаемое значение критерия:

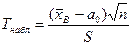
- если 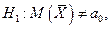то критическая точка t_{двуст.кр.} находится по таблице критических точек распределения Стьюдента по известным α и k = n – 1.

Если | T_набл | < t_{двуст.кр.}, то нулевая гипотеза принимается.

Если | T_набл | > t_{двуст.кр.}, то нулевая гипотеза отвергается.

- если 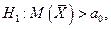, то по соответствующей таблице находят t_{правост.кр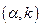} – критическую точку правосторонней критической области. Нулевая гипотеза принимается, если T_наб < t_{правост.кр.}.

- при конкурирующей гипотезе 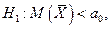критическая область является левосторонней, и нулевая гипотеза принимается при условии T_набл > - t_{правост.кр.}. Если

T_набл < - t_{правост.кр.}., нулевую гипотезу отвергают.