Доверительный интервал для оценки математического ожидания нормального распределения при неизвестной дисперсии

Если известно, что исследуемая случайная величина Х распределена по нормальному закону с неизвестным средним квадратическим отклонением, то для поиска доверительного интервала для ее математического ожидания построим новую случайную величину

,

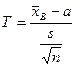где 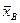- выборочное среднее, 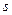– исправленная дисперсия, п – объем выборки. Эта случайная величина, возможные значения которой будем обозначать t, имеет распределение Стьюдента с 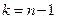степенями свободы.

Так как плотность распределения Стьюдента , где 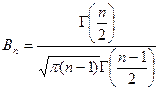, явным образом не зависит от а и 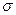, можно задать вероятность ее попадания в некоторый интервал , учитывая четность плотности распределения, следующим образом: 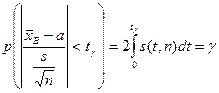. Отсюда получаем:

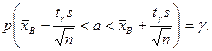
Таким образом, получен доверительный интервал для а, где 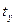можно найти по соответствующей таблице при заданных п и .

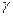Пример. Пусть объем выборки 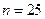, 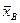= 3, 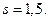Найдем доверительный интервал для а при Из таблицы находим, что 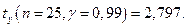Тогда , или 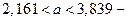доверительный интервал, в который попадает а с вероятностью 0,99.