Доверительные интервалы для оценки среднего квадратического отклонения

нормального распределения.

Найдём для среднего квадратического отклонения нормально распределенной случайной величины доверительный интервал вида где s – исправленное выборочное среднее квадратическое отклонение, а для выполняется условие: Запишем это неравенство в виде: или, обозначив , в виде

. (5.1)

Рассмотрим случайную величину , определяемую по формуле

,

которая распределена по закону «хи-квадрат» с степенями свободы. Плотность ее распределения

не зависит от оцениваемого параметра 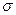, а зависит только от объема выборки п. Преобразуем неравенство (5.1) так, чтобы оно приняло вид . Вероятность выполнения этого неравенства равна доверительной вероятности γ, следовательно,

Предположим, что 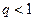, тогда неравенство (5.1) можно записать в виде

,

или, после умножения на , в виде . Следовательно, . Тогда

Существуют таблицы для распределения «хи-квадрат», из которых можно найти q по заданным п и 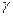, не решая этого уравнения. Таким образом, вычислив по выборке значение s и определив по таблице значение q, можно найти доверительный интервал (5.1), в который значение σ попадает с заданной вероятностью .

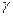Замечание. Если , то с учетом условия доверительный интервал для 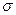будет иметь границы

.

Пример. Пусть п = 20, s = 1,3. Найдем доверительный интервал для σ при заданной надежности 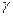=0,95. Из соответствующей таблицы находим q (n = 20, γ = 0,95) = 0,37. Следовательно, границы доверительного интервала: 1,3(1-0,37) = 0,819 и 1,3(1+0,37) = 1,781. Следовательно, с вероятностью 0,95.