Примеры решения задач. Пример 1. Из генеральной совокупности извлечена выборка xi mi

Пример 1. Из генеральной совокупности извлечена выборка

xi
mi

Найти несмещенные оценки генеральной средней и дисперсии.

Решение. 1) n=16+12+8+14=50.

Несмещенной оценкой генеральной средней является выборочная средняя =

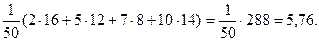
2) Несмещенной оценкой генеральной дисперсии является исправленная дисперсия

.

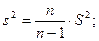
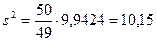Пример 2. Случайная величина Х (число нестандартных изделий в партии изделий) распределена по закону Пуассона. Распределение задано таблицей

xi
mi

Найти методом моментов точечную оценку неизвестного параметра λ распределения Пуассона.

Решение. Согласно методу моментов для распределения с одним параметром, его оценка определяется из решения уравнения

М(х)= .

Математическое ожидание случайной величины, распределенной по закону Пуассона равно М(х)=λ. Следовательно, получаем λ*= .

Итак, для оценки параметра λ необходимо найти выборочное среднее арифметическое значение:

n=132+43+20+3+2=200;

=

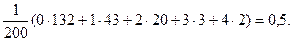
Пример 3. Найти методом моментов по выборке х₁, х₂, …, х_n точечные оценки неизвестных параметров а и b равномерного распределения.

Решение. Так как равномерное распределение определяется двумя параметрами, метод моментов сводится к решению системы уравнений

.

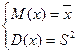Поскольку, при равномерном распределении М(х)= 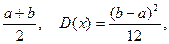для определения оценок параметров a и b необходимо решить систему уравнений

;

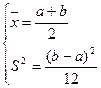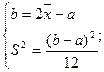
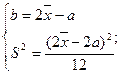
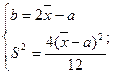
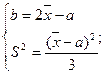
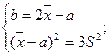
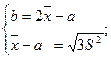
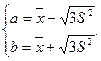
Итак,

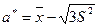
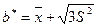
Пример 4. Найти методом наибольшего правдоподобия точечную оценку неизвестного параметра р биноминального распределения.

Решение. Запишем функцию правдоподобия для дискретной биноминально распределенной случайной величины. Так как при биноминальном распределении 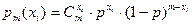, где n – число опытов, m – количество испытаний в одном опыте, следовательно, функция правдоподобия имеет вид · ·…· =

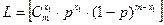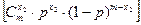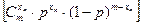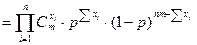
Для простоты вычиcлений возьмем от функции L натуральный логарифм:

lnL=ln(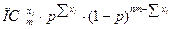)=ln(П ) +

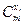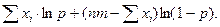
Для нахождения экстремума функции ln(L) продифференцируем ее по переменной р:

Далее, для вычисления критических точек решим уравнение

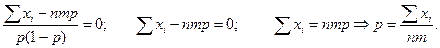(3.1)

Чтобы определить, будет ли полученное значение р являться точкой максимума, найдем вторую производную функции ln(L), и ее значение в точке 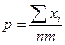. Если это значение меньше нуля то, полученная критическая точка, является точкой максимума.

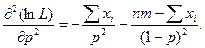
Так как, 0≤р≤1, то согласно условию (3.1), получаем 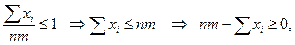и из определения биноминального распределения поэтому 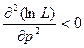для любого р, в том числе и для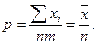

Итак, значение 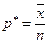является максимальным для функции правдоподобия, а, следовательно, и оценкой неизвестного параметра р биноминально распределенной случайной величины.

Пример 5. Найти методом наибольшего правдоподобия оценки параметров а и σ нормального распределения.

Решение. Для определения оценок параметров а и σ решим систему дифференциальных уравнений:

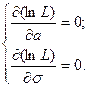
Так как функция плотности распределения нормальной случайной величины имеет вид 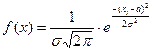, следовательно, функция правдоподобия … =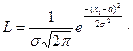

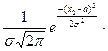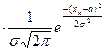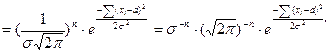
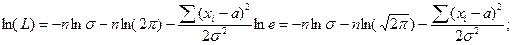
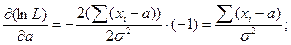
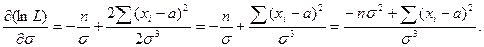
Тогда, 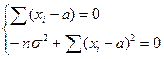; ; 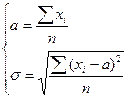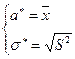- оценки параметров нормального распределения.