Решение. Для исследования функции и построения ее графика применяется следующая схема:

Для исследования функции и построения ее графика применяется следующая схема:

1) найти область определения функции;

2) определить точки разрыва функции и выяснить их характер;

3) исследовать функцию на четность и нечетность, периодичность;

4) найти точки пересечения графика функции с осями координат;

5) найти асимптоты графика функции;

6) найти промежутки возрастания и убывания, точки экстремума;

7) найти интервалы выпуклости и вогнутости, точки перегиба;

8) для уточнения графика найти дополнительные точки;

9) по результатам исследования построить график функции.

Применим вышеуказанную схему для исследования данной функции:

1) область определения функции ;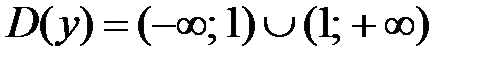

2) функция не определена в точке . Следовательно, есть точка разрыва функции. Исследуем характер точки разрыва, для чего найдем односторонние пределы функции в этой точке:

.

Следовательно, точка разрыва второго рода;

3) функция не является ни четной, ни нечетной, так как

;

4) найдем точки пересечения с осью Ох, решив уравнение :

.

Точка 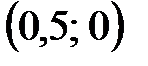– точка пересечения графика с осью Ох.

Точки пересечения с осью Оy найдем, положив : . Точка (0; –1) – точка пересечения графика с осью Оу;

5) так как точка – точка разрыва второго рода, то прямая – вертикальная асимптота.

Найдем наклонные асимптоты вида , где

, .

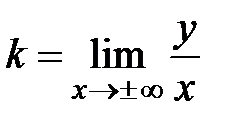Тогда

Следовательно, – горизонтальная асимптота;

6) определим промежутки возрастания, убывания функции и точки экстремума, для чего найдем критические точки первого рода:

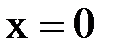Так как при , следовательно является критической (стационарной) точкой. Других критических точек нет, так как точка , в которой функция имеет бесконечную производную, не принадлежит .

Полученные данные занесем в таблицу 7.

Таблица 7

x
	-		+		-
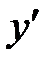
y	Убывает		Возрастает	Не существует	Убывает

Функция убывает на интервалах и возрастает на интервале . Следовательно, точка есть точка минимума;

7) определим промежутки выпуклости, вогнутости и точки перегиба, для чего найдем критические точки второго рода:

при , следовательно является критической точкой. Других критических точек нет, так как точка , в которой функция имеет бесконечную вторую производную, не принадлежит . Полученные данные занесем в таблицу 8.

Таблица 8

x
	-		+		+
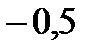
y	Выпукла		Вогнута	Не существует	Вогнута

Функция выпукла на интервале и вогнута на интервалах . Точка есть точка перегиба графика функции;

8) для уточнения графика найдем дополнительные точки:

;

9) по полученным данным строим график функции (рисунок 1).

Рисунок 1 – График функции