 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Решение. 1 Уравнение прямой, проходящей через две точки , имеет вид:
|
|
1 Уравнение прямой, проходящей через две точки 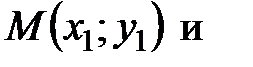
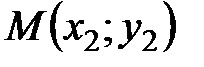 , имеет вид:
, имеет вид:
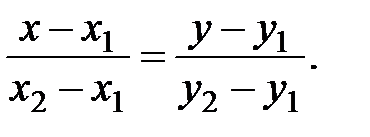
Тогда 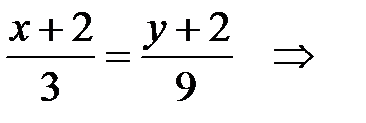
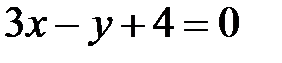 - уравнение прямой (стороны) АВ.
- уравнение прямой (стороны) АВ.
2 Уравнение высоты СН получим, воспользовавшись уравнением прямой, проходящей через точку 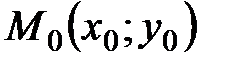 параллельно вектору
параллельно вектору 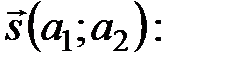
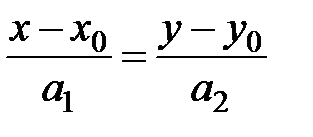 .
.
Так как 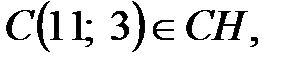
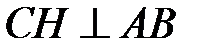 , то нормальный вектор
, то нормальный вектор 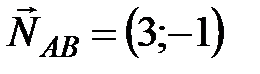 является направляющим для прямой СН, т.е.
является направляющим для прямой СН, т.е. 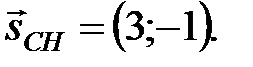 Следовательно,
Следовательно, 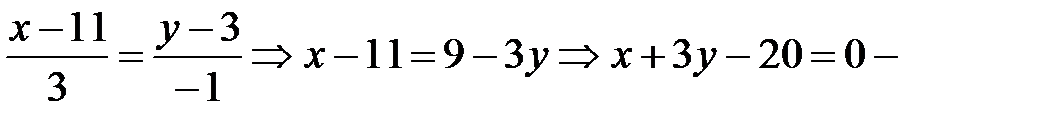 уравнение стороны СН.
уравнение стороны СН.
Длину высоты СН найдем как расстояние от точки С до прямой АВ, используя формулу
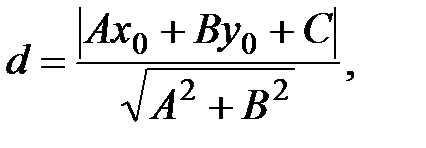
где 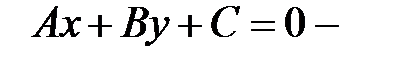 уравнение данной прямой;
уравнение данной прямой;
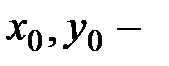 координаты данной точки.
координаты данной точки.
Имеем:
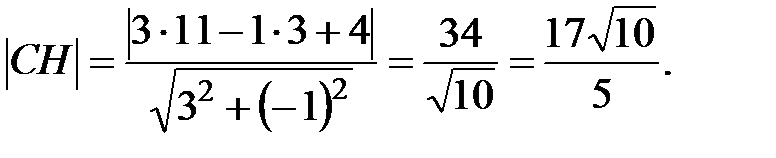
3 Так как АМ – медиана, то точка М – середина отрезка ВС. Координаты середины отрезка находим по формулам:
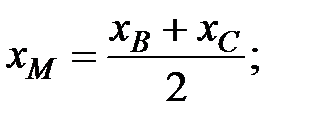
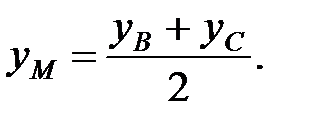
Тогда 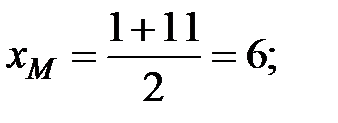
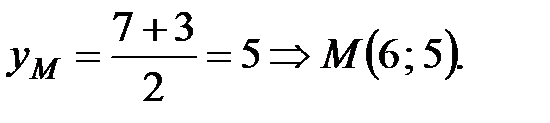
Уравнение прямой АМ:
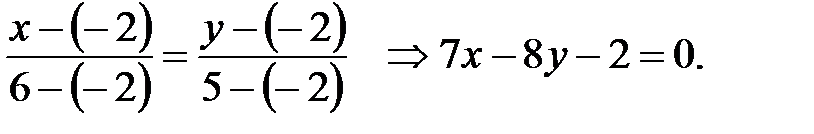
Длину медианы АМ найдем как расстояние между двумя точками, используя формулу
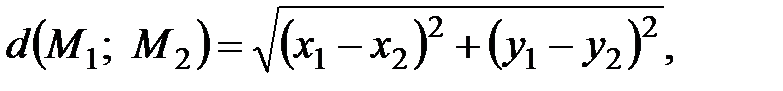
где 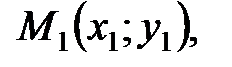
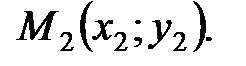
Имеем 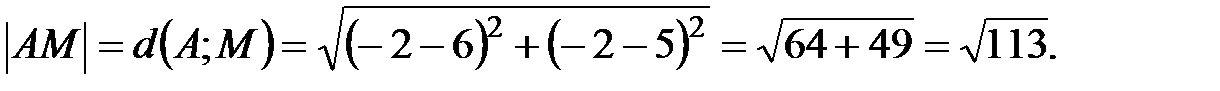
4 Найдем точку N пересечения медианы АМ и высоты СН, решив систему:
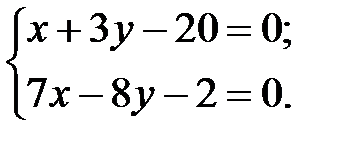
Тогда 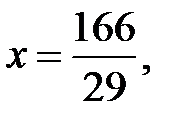
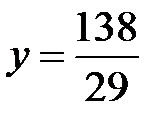 и N=
и N= 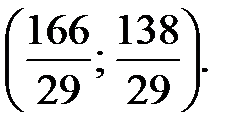
5 Так как прямая, проходящая через точку С параллельно прямой АВ, имеет тот же нормальный вектор, что и прямая АВ, т.е. 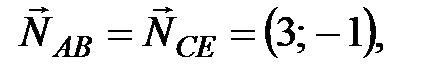 то уравнение прямой СЕ запишем, используя уравнение прямой, проходящей через точку
то уравнение прямой СЕ запишем, используя уравнение прямой, проходящей через точку 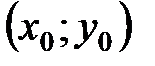 перпендикулярно нормальному вектору
перпендикулярно нормальному вектору 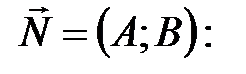
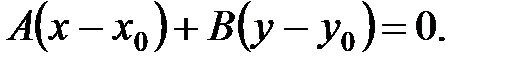
Следовательно, 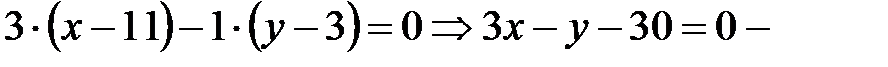 уравнение стороны АВ.
уравнение стороны АВ.
6 Для нахождения внутреннего угла А воспользуемся формулой
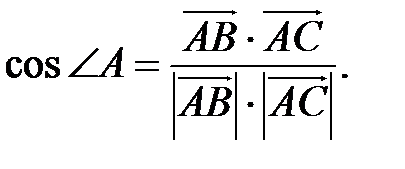
Так как 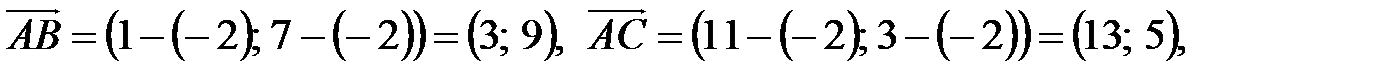
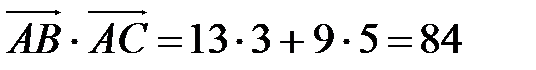 ,
, 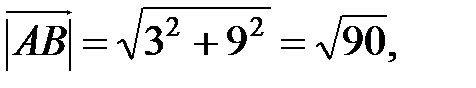
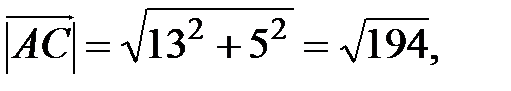 то
то 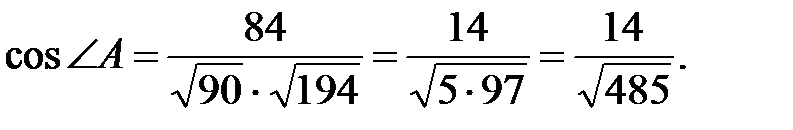
Следовательно, 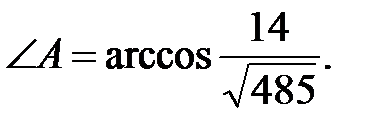
Ответ: 1) АС: 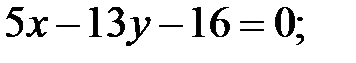 2) СН:
2) СН: 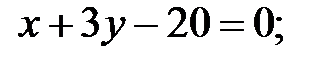
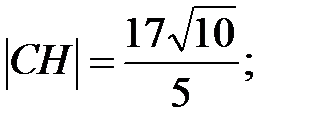
3) АМ: 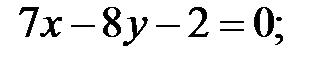
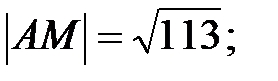 4) N
4) N 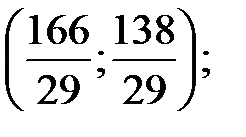 5) СЕ:
5) СЕ: 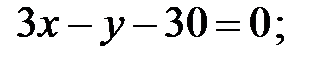
6) 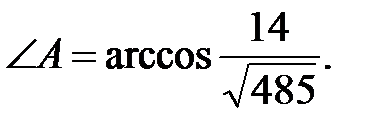
Дата публикования: 2015-10-09; Прочитано: 290 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
