Решение. 1 Решим систему по формулам Крамера:

1 Решим систему по формулам Крамера:

,

где главный определитель системы, составленный из коэффициентов при неизвестных;

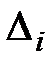
определитель системы, полученный путем замены -го столбца главного определителя системы столбцом свободных членов.

Таким образом, , , .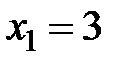

2 Решим СЛАУ матричным способом.

Обозначим:

; ; .

Тогда данную систему можно записать в виде откуда ( обратная матрица по отношению к матрице ).

Найдем по следующей формуле:

,

где − алгебраические дополнения к соответствующим элементам матрицы А: 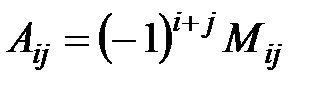, ( миноры, соответствующие элементам матрицы А).

Обратная матрица имеет вид:

.

Тогда .

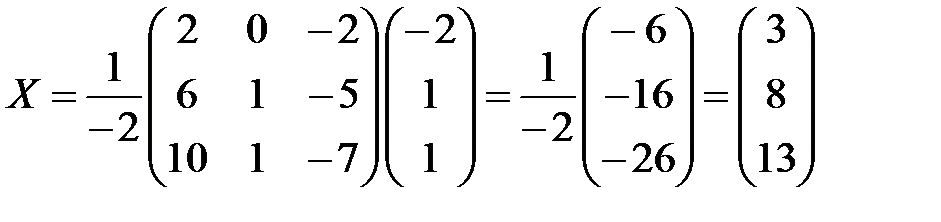Итак, решение системы:

3 Решим СЛАУ методом Гаусса.

С помощью элементарных преобразований строк расширенную матрицу системы приведем к следующему виду:

Так как , то система совместна и имеет решение. Полученной матрице соответствует система

которая эквивалентна исходной. Из данной системы следует, что

Ответ: