 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Случайная погрешность отдельного измерения
|
|
Колебания случайной погрешности, кажущиеся сначала совершенно беспорядочными, тем не менее, подчиняются в статистическом смысле известным законам.
Если показания какого-либо измерительного прибора, являющиеся сами по себе непрерывными, разбить на интервалы определённой ширины 
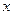 и вычислить относительную частоту попадания показаний в отдельные интервалы при повторных измерениях, то можно получить гистограмму.
и вычислить относительную частоту попадания показаний в отдельные интервалы при повторных измерениях, то можно получить гистограмму.
При достаточно большом значении n это изображение является представительным, т.е. относительная частота стремится к некоторому пределу и перестаёт зависеть от n.
Если имеется достаточно большое число показаний, то можно улучшать гистограмму, уменьшая ширину интервалов 
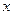 . Тогда при предельном переходе
. Тогда при предельном переходе 
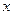
 и n
и n  ступенчатая функция гистограммы переходит в общем случае в непрерывную функцию – плотность распределения (плотность вероятности, дифференциальную функцию распределения) h (
ступенчатая функция гистограммы переходит в общем случае в непрерывную функцию – плотность распределения (плотность вероятности, дифференциальную функцию распределения) h (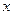 )
)
h (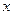 ) =
) = 
Основываясь на определении плотности распределения, можно установить её прямую связь с функцией распределения. Вероятность того, что измеряемое значение 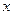 попадает в интервал
попадает в интервал 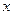 1 < x £ x 2, определяется площадью F, лежащей под графиком плотности распределения вероятности в этом диапазоне:
1 < x £ x 2, определяется площадью F, лежащей под графиком плотности распределения вероятности в этом диапазоне:
P (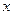 1 <
1 < 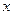 £
£ 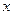 2) =
2) = 
В частном случае имеем
P (-  <
< 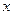 £ +
£ +  ) =
) = 


Часто при обработке результатов измерения представляет интерес вероятность того, что измеренная величина окажется меньше заданного предела 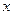 1:
1:
P (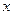 ) = P (
) = P (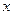 £
£ 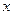 1) =
1) =  .
.
При -  <
< 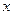 £ +
£ +  функция распределения изменяется от 0 до 1. В связи с тем, что функция распределения Р(
функция распределения изменяется от 0 до 1. В связи с тем, что функция распределения Р(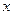 ) определяется как интеграл плотности h (
) определяется как интеграл плотности h (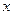 ), её часто называют также интегральной функцией распределения.
), её часто называют также интегральной функцией распределения.
Аналогичным образом определяется вероятность того, что измеренная величина окажется больше, чем 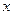 1:
1:
P (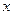 >
> 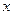 1) =
1) = 
Среди множества функций распределения особое место для измерительной техники занимает нормальное распределение (распределение Гаусса).
Плотность вероятности нормального распределения определяется следующим уравнением:
h (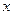 ) =
) =  -
-  <
< 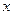 £ +
£ + 
Нормальное распределение характеризуется, кроме математического ожидания 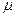 , ещё только одним параметром
, ещё только одним параметром  - среднеквадратичным (стандартным) отклонением.
- среднеквадратичным (стандартным) отклонением.
При известном среднеквадратичном отклонении  можно вычислить вероятность того, что случайная погрешность Еаi – отклонение показания отдельного измерения от математического ожидания – будет меньше заданного граничного значения с. Эта вероятность
можно вычислить вероятность того, что случайная погрешность Еаi – отклонение показания отдельного измерения от математического ожидания – будет меньше заданного граничного значения с. Эта вероятность
Р ( £с) = 2
£с) = 2 
называется доверительной вероятностью (статистической надёжностью).
При известном значении  (рис.5.1) можно на основании единственного измерения указать верхнюю и нижнюю границы математического ожидания:
(рис.5.1) можно на основании единственного измерения указать верхнюю и нижнюю границы математического ожидания:

 или
или 
Математическое ожидание с доверительной вероятностью Р(%) лежит внутри этих границ. Интервал между этими границами называется доверительным интервалом математического ожидания.
Математическое ожидание определяется следующим образом:
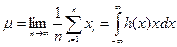
Эта величина соответствует первому моменту плотности распределения – абсциссе центра тяжести площади между зависимостью плотности распределения и осью абсцисс.
Площадь фигуры, очерченной зависимостью  , равна единице.
, равна единице.
В качестве оценки для 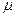 используется среднее значение
используется среднее значение  :
:

Среднеквадратичное отклонение  определяется из формулы
определяется из формулы

Величина  , называемая дисперсией, соответствует второму моменту («моменту инерции») плотности распределения вероятностей.
, называемая дисперсией, соответствует второму моменту («моменту инерции») плотности распределения вероятностей.
В качестве оценки среднеквадратичного отклонения  используется рассеяние S, определяемое по формуле
используется рассеяние S, определяемое по формуле
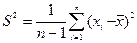
Дата публикования: 2015-10-09; Прочитано: 160 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
