А) Случай одной независимой переменной

Пусть задано дифференциальное выражение с обыкновенными производными

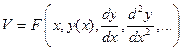(1)

Здесь – независимая переменная, 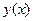– функция, которая со своими производными определена на некотором интервале оси .

Цель замены старых переменных 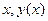– получить возможно более простое дифференциальное выражение.

Рассмотрим преобразование выражения (1) сначала при замене только независимой переменной .

Введем новую независимую переменную 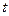соотношением

(2)

Функция предполагается непрерывной со всеми своими производными требуемого порядка, кроме того, предполагается, что .

При замене (2) функция 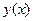превратится в функцию . Задача состоит в переходе

.

Далее нужно выразить производные от функции по аргументу через производные от новой функции по аргументу . Заметим, что нам задана зависимость (2), не разрешенная относительно аргумента , но определяющая обратную функцию .

Запишем тождественное преобразование

(3)

Дифференцируем это тождество по аргументу : .

По правилу дифференцирования обратной функции находим . Значит,

(4)

Таким образом, при переходе от производной по старому аргументу к производной по новому аргументу появляется «переходный» множитель .

Дифференцируем (4) по :

Опять появился множитель .

По правилу дифференцирования частного находим

.

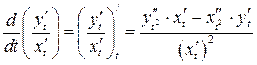Значит,

. (5)

Аналогично вычисляются последующие производные. В результате заданное выражение 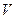преобразуется к виду

.

Нет необходимости запоминать формулы (4), (5) и т.д. Следует просто всякий раз при конкретном задании формулы преобразования (2) находить производные по изложенному правилу.

Пример 1. Преобразовать дифференциальное выражение

к новой независимой переменной , полагая .

Решение. Дифференцируем тождество :

.

Здесь учтено, что .

Далее:

.

Подставим найденные производные в выражение :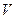

.

Мы видим, насколько упростилось выражение 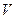. Если было задано уравнение 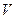=0, то после такой замены получается уравнение с постоянными коэффициентами при и . ☻

Рассмотрим преобразование выражения (1) при замене только функции .

Пусть функция заменяется новой функцией , связанной с соотношением

(6)

Задача состоит в переходе

.

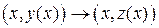Запишем тождественное преобразование

Дифференцируем это тождество по аргументу :

Появился множитель . Продолжаем дифференцировать:

и т.д.

После подстановки выражение 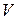преобразуется к виду

.

Пример 2. Преобразовать уравнение

к новой функции , если .

Решение. Дифференцируем тождество по :

.

Здесь учтено, что .

Продолжаем дифференцировать:

.

В результате выражение 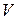преобразуется к виду:

.

Значит, уравнение приняло вид . Дифференциальное уравнение вида называется гармоническим осциллятором; его решением, как легко проверить, является функция

.

В нашем случае . ☻

Рассмотрим преобразование выражения (1) в общем случае, то есть при замене и аргумента, и функции.

Пусть старые переменные связаны с новыми переменными соотношениями

(7)

Задача состоит в переходе . Чтобы пересчитать производные, надо последовательно дифференцировать по аргументу тождество

.

Пример 3. Преобразовать уравнение

,

полагая .

Решение. Первый способ. Запишем тождество .

Дифференцируем его по аргументу :

Заметим, что заданные зависимости между старыми и новыми переменными разрешены относительно . Вычислим производные:

и подставим их в продифференцированное тождество:

. (8)

Отсюда находим первую производную .

Дифференцируем по соотношение (8):

.

Подставим в правую часть найденную производную :

.

Отсюда находим вторую производную . Остается подставить производные в заданное уравнение:

.

Второй способ. Разрешим зависимости между старыми и новыми переменными относительно : . Будем последовательно дифференцировать тождество по аргументу :

.

Вычислим производные и подставим их в продифференцированное тождество:

.

Получили знакомый результат. Продолжаем дифференцировать по :

Отсюда находим – и этот результат уже был получен. Заданное уравнение предложенная замена преобразует к виду .☻

Пример 4. Задана плоская линия . Преобразовать выражение для кривизны этой линии к полярным координатам , полагая

. (9)

Решение. Задача состоит в переходе . Дифференцируем тождество по аргументу :

Вычислим производные и подставим в продифференцированное тождество:

, (10)

Отсюда находим первую производную

.

Продолжаем дифференцировать по аргументу – удобнее это делать с выражением (10):

Получаем

Отсюда с учетом уже найденной первой производной после несложных преобразований получаем вторую производную

.

Остается подставить найденные и в выражение для кривизны. Получим кривизну линии в полярных координатах:

.

Замечание. Можно было соотношения (9) разрешить относительно переменных : и дифференцировать по аргументу тождество

. ☻